Fourier Baron Jean Baptiste Joseph Fourier (1768-1830)
Baron Jean Baptiste Joseph Fourier (1768-1830)
französischer Mathematiker und Physiker
-Entwicklung Baron Jean Baptiste Joseph Fourier (1768-1830)
Baron Jean Baptiste Joseph Fourier (1768-1830)französischer Mathematiker und Physiker
 Baron Jean Baptiste Joseph Fourier (1768-1830)
Baron Jean Baptiste Joseph Fourier (1768-1830)Inhalt
3. Bestimmung der Koeffizienten
6. kontinuierliche Fouriertransformation
8. Anwendungen in der Signalverarbeitung
1. Einführung
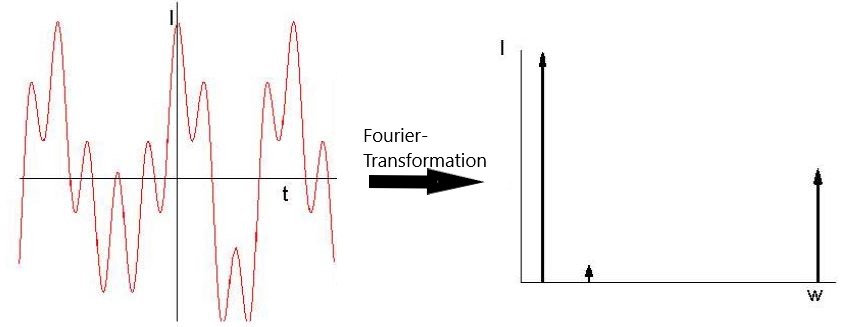 Aus physikalischer Sicht geht es darum, ein zeitabhängiges Signal in ein frequenzartiges Signal umzuwandeln.
Aus physikalischer Sicht geht es darum, ein zeitabhängiges Signal in ein frequenzartiges Signal umzuwandeln.2. Orthogonalitätsrelationen
3. Bestimmung der Koeffizienten
4. Beispiele
| 1. | Es soll eine Fourier-Analyse der Kipp- oder Sägezahnschwingung erfolgen: f(x) = \(\begin{cases} x,~falls~ -\pi < x < \pi \\0, ~falls~ x = \pm\pi \end{cases}\) a) Zeichnen Sie den Graphen der Funktion f. b) Die Darstellung der Funktion f als trigonometrisches Polynom ist $$f(x)~ =~ \frac{a_0}{2}+\sum_{n=1}^{\infty}(a_n \cdot cos(nx)+b_n \cdot sin(nx))$$ mit \(a_0=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)~dx\) sowie \(a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cdot cos(nx)~dx\) und \(b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cdot sin(nx)~dx\). Begründen Sie, dass nur die bn bestimmt werden müssen, denn an = 0. c) Zeigen Sie, dass für bn mit n > 0 gilt: \(b_n~=~-\frac{2}{\pi}\frac{\pi \cdot cos(n \pi)}{n}~=~2\frac{(-1)^{n+1}}{n}\). Hinweis: Es gilt \(\int x\cdot sin(ax)~dx~=~\frac{sin(a x)}{a}-\frac{x \cdot cos(a\cdot x)}{a}\). d) Geben Sie die ersten fünf Summanden der Fourierdarstellung von f an.
zu a)  zu b)
zu b)Die Periode ist T = 2π. f ist eine punktsymmetrische Funktion, cos eine achsensymmetrische Funktion, das Produkt beider Funktionen ist punktsymmetrisch. Die Fläche unter dem Graphen einer ungeraden Funktion ist über eine Periode Null. Deshalb gilt: an = 0. zu c) \(b_n~=~\frac{2}{2\pi}\int_{-\pi}^{\pi} x~sin~(\frac{2\pi}{2\pi}nx)~dx~=~\frac{1}{\pi}\left[\frac{sin(nx)}{n}-\frac{x\cdot cos(n\cdot x)}{n}\right]_{-\pi}^{\pi}\) \(~~~~=~\frac{1}{\pi}\left[(0-\frac{\pi\cdot(-1)^n}{n})-(0-\frac{-\pi\cdot(-1)^n}{n})\right]~=~\frac{1}{\pi}(-2\frac{\pi\cdot(-1)^n}{n})~=~\frac{2}{n}(-1)^{n+1}\) zu d)  Die Fourierdarstellung der Kippschwingung lautet dann:
Die Fourierdarstellung der Kippschwingung lautet dann:$$f(x)~\approx~2sin ~x - sin(2x)+\frac{2}{3}sin(3x)-\frac{1}{2}sin(4x)+\frac{2}{5}sin(5x)-...$$ |
| 2. | a) Führen Sie für eine Rechteck-Schwingung der Amplitude A sowie der Periode T eine Fourier-Analyse durch. b) Führen Sie für eine Dreieck-Schwingung der Amplitude A sowie der Periode T eine Fourier-Analyse durch. c) Führen Sie für die Funktion f(x) = x2 mit der Periode T = 2π eine Fourier-Analyse durch.
zu a) Rechteckschwingung: f(x) = \(\begin{cases} -1,~falls~ -\frac{T}{2} < x < 0 \\0, ~falls~ -\frac{T}{2};0;\frac{T}{2} \\1, ~falls~0 < x < \frac{T}{2} \end{cases}\) Die Funktion f ist punktsymmetrisch, deshalb werden nur die bn berechnet. \(b_n~=~\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)~sin~(\frac{2\pi}{T}nx)~dx~=~\frac{4}{T}\int_{0}^{\frac{T}{2}}f(x)~sin~(\frac{2\pi}{T}nx)~dx\) , da f(x)⋅sin x achsensymmetrisch f(x) einsetzen (und n > 0): \(b_n~=~\frac{4}{T}\int_{0}^{\frac{T}{2}}1\cdot~sin~(\frac{2\pi}{T}nx)~dx~=~\frac{4}{T}\left[-\frac{T}{2\pi n} cos (\frac{2\pi}{T}nx)\right]_{0}^{\frac{T}{2}}\) \(~~~~=~-\frac{4}{2\pi n} (cos~(\pi n)~-~1)~=~\begin{cases} 0~,~falls~n~gerade \\ \frac{4}{\pi n}~,~falls~n~ungerade \end{cases}\) Die Fourierreihe für die Rechteckschwingung lautet: $$f(x)~ =~ \frac{4}{(2n-1)\pi}\sum_{n=1}^{\infty} sin(\frac{2\pi}{T}(2n-1)x)$$ Falls T = 2π, dann $$f(x)~ =~ \frac{4}{\pi} ~(sin~x~+~\frac{1}{3}sin(3x)~+~\frac{1}{5}sin{5x}~+~\frac{1}{7}sin(7x)~ + ~...)$$ 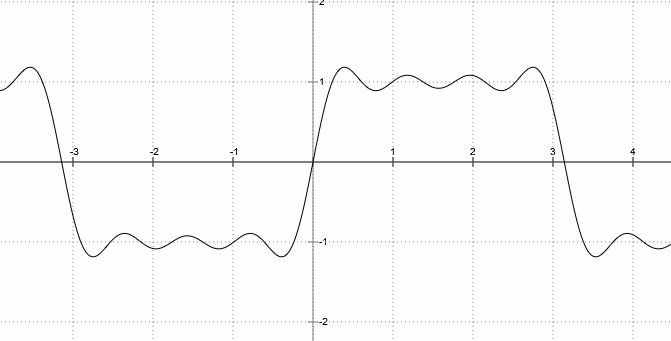 Um die Amplitude A abzubilden, wird der Funktionsterm mit A multipliziert. Im Bild: Näherung für n = 4. Anmerkung: Gibbsches Phänomen: Wenn die Koeffizienten nicht schnell genug gegen Null gehen, lässt häufig das Konvergenzverhalten an den Unstetigkeitsstellen nach. zu b) Dreieckschwingung: f(x) = |x| im Intervall [\(-\frac{T}{2},\frac{T}{2}\)].  Die Funktion f ist achsensymmetrisch, deshalb werden nur die an berechnet.
Die Funktion f ist achsensymmetrisch, deshalb werden nur die an berechnet.Es gilt: \(\int x~cos(ax)~dx~=~\frac{1}{a}x~sin(ax)~+~\frac{1}{a^2}cos(ax)~+~c\) $$a_0~=~\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(x)\cdot 1~dx~=~\frac{2}{T}\int_{0}^{\frac{T}{2}} x~dx~=~\frac{2}{T}\left[\frac{1}{2}x^2\right]_{0}^{\frac{T}{2}}~=~\frac{T}{4}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ $$a_n~=~\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}} f(x)~cos~(\frac{2\pi}{T}nx)~dx~=~\frac{4}{T}\int_{0}^{\frac{T}{2}} x~cos~(\frac{2\pi}{T}nx)~dx~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ $$=~\frac{4}{T}\left[\frac{T}{2\pi n}x~sin(\frac{2\pi}{T}nx)+\frac{T^2}{4\pi^2n^2}cos(\frac{2\pi}{T}nx)\right]_{0}^{\frac{T}{2}}~=~\frac{4}{T}\left[(0+\frac{T^2}{4\pi^2n^2}cos(\pi n))-(0+\frac{T^2}{4\pi^2n^2}) \right]$$ daraus folgt: $$a_n~ =~ \begin{cases}0~,~falls~n~gerade\\-\frac{2T}{\pi^2n^2}~,~falls~n~ungerade \end{cases}~~~~~~~~~~~~~~~~~~~~~~~~~~$$ Falls T = 2π, dann $$f(x)~=~\frac{\pi}{2} ~-~\frac{4}{\pi}(cos~x~+~\frac{1}{9}cos(3x)~+~\frac{1}{25}cos(5x)~+~\frac{1}{49}cos(7x)~ + ~...)$$ Um die Amplitude A abzubilden, wird der Funktionsterm mit A multipliziert. zu c) Die Funktion ist achsensymmetrisch. Deshalb müssen nur die an berechnet werden. Mit T = 2π: $$a_0~=~\frac{1}{2\pi}\int_{-\pi}^{\pi}x^2~dx~=~\frac{1}{2\pi}\left[\frac{1}{3}x^3\right]_{-\pi}^{\pi}~=~\frac{1}{3}\pi^{2}~~~~~~~~~~~~~~~~~~~~~~~~$$ $$a_n~=~\frac{1}{\pi}\int_{-\pi}^{\pi} x^2~cos~(nx)~dx~=~\frac{2}{\pi}\left[\frac{2x}{n^2}cos(nx)+\left(\frac{x^2}{n}-\frac{2}{n^3}\right)sin(nx)\right]_{0}^{\pi}$$ $$\rightarrow~~a_n~=~\frac{2}{\pi}\left[\frac{2\pi}{n^2}(-1)^n \right]~=~\frac{4}{n^2}(-1)^n~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$$ Insgesamt für T = 2π: $$f(x)~=~x^2~=~\frac{\pi^2}{3}~+~4\sum_{n=1}^{\infty}\frac{(-1)^n}{n^2}cos(nx)~=~\frac{\pi^2}{3}~+~4\left(-cos(x)~+\frac{1}{4}cos(2x)~-~\frac{1}{9}cos(3x)~+~...\right)$$ |
5. komplexe Schreibweise
6. kontinuierliche Fouriertransformation
 Bisher wurden periodische Signale mit der Periode T betrachtet.
Bisher wurden periodische Signale mit der Periode T betrachtet.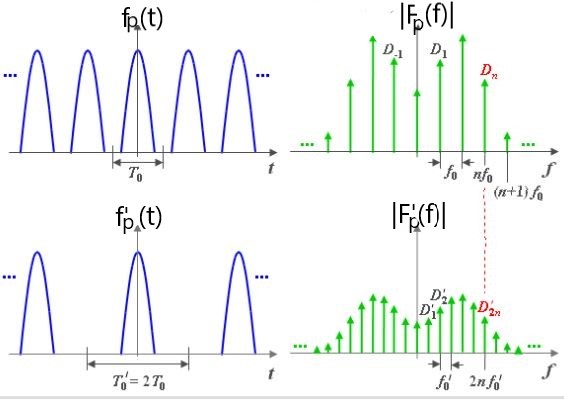
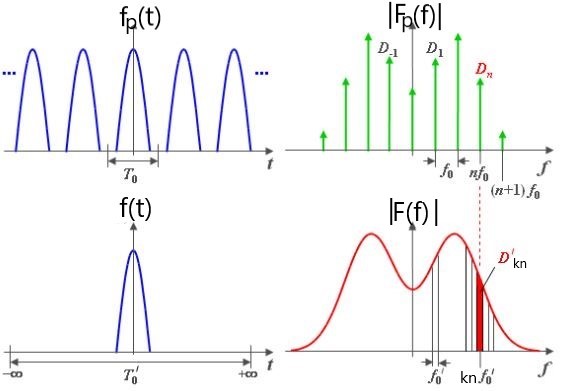
 f(t) = \(\begin{cases} e^{-\lambda t},~falls~ t\ge 0 \\0 ~~~sonst \end{cases}\)
f(t) = \(\begin{cases} e^{-\lambda t},~falls~ t\ge 0 \\0 ~~~sonst \end{cases}\)7. Fourier und π
8. Anwendungen in der Signalverarbeitung
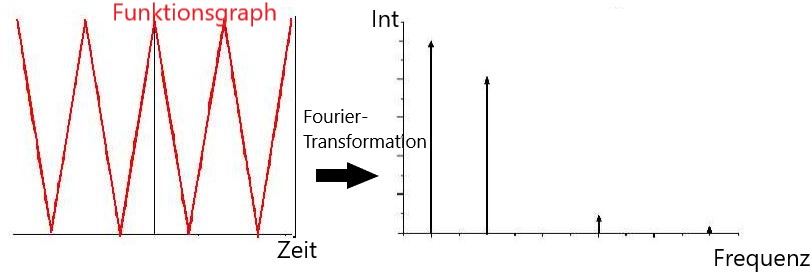 Ein Signal wird abgetastet (sampling). Die Signalfunktion besteht somit aus mehreren diskreten Werten. Die Fensterlänge N gibt die Anzahl der Werte an, die jeweils für eine Analyse oder
Bearbeitung verwendet wird. Mittels einer sogenannten Fensterfunktion (das kann auch eine einfache Rechteckfunktion sein) werden die Werte des Signals ausgewählt -
wie bei der Rechteckfunktion - oder je nach Fensterfunktion verändert. Diese Werte können durch eine diskrete Fouriertransformation in ihre spektralen Anteile zerlegt werden.
Ein Signal wird abgetastet (sampling). Die Signalfunktion besteht somit aus mehreren diskreten Werten. Die Fensterlänge N gibt die Anzahl der Werte an, die jeweils für eine Analyse oder
Bearbeitung verwendet wird. Mittels einer sogenannten Fensterfunktion (das kann auch eine einfache Rechteckfunktion sein) werden die Werte des Signals ausgewählt -
wie bei der Rechteckfunktion - oder je nach Fensterfunktion verändert. Diese Werte können durch eine diskrete Fouriertransformation in ihre spektralen Anteile zerlegt werden.