Die Lösung vieler Anwendungen (z.B. Extremwertaufgaben) lässt sich auf das Auffinden von Nullstellen zurückführen. In den meisten Fällen gibt es aber keine geschlossenen Lösungen. In praktischen Fällen reicht es aber aus, einen Näherungswert für die Nullstellen anzugeben. Man gibt dabei eine bestimmte Genauigkeit ε vor - beispielsweise auf 6 Nachkommastellen genau: ε = 0,000001.
Man beginnt mit einem oder mehreren Startwerten und gibt die Genauigkeit ε vor. Dann wird in einem Iterationsschritt ein neuer Näherungswert errechnet, mit dem der nächste (bessere) Näherungswert ermittelt wird. Dies wird bis zur gewünschten Genauigkeit wiederholt.
Ob die jeweiligen Verfahren sich wirklich an eine Nullstelle annähern - also konvergieren - hängt von den Startwerten ab. Wichtig für die Beurteilung der einzelnen Verfahren ist die Konvergenzgeschwindigkeit dieser Verfahren - wie hoch ist der Rechenaufwand pro Rechenschritt und wieviele Iterationsschritte sind bis zum Erreichen der gewünschten Genauigkeit nötig.
Wir gehen davon aus, dass die zu untersuchende Funktion stetig ist - also keine Sprünge macht - und eine Nullstelle existiert.
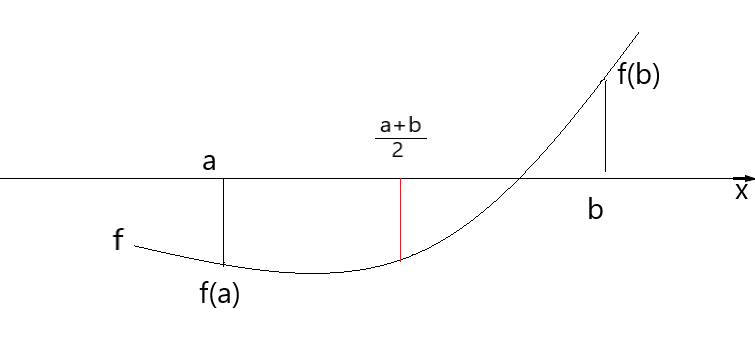
Gegeben ist eine stetige Funktion f.
Man benötigt zwei Startwerte a und b mit der Bedingung f(a) · f(b) < 0 sowie die Genauigkeit ε. Da die Funktionswerte wegen der Bedingung unterschiedliche Vorzeichen haben, folgt, dass eine Nullstelle im Intervall [a,b] existiert. Nun wird der Mittelwert gebildet, der Funktionswert f(z) berechnet und je nach Vorzeichen von f(z) entweder a oder b durch z ersetzt.
Durch diesen Schritt wird das Intervall halbiert. Dies wird solange wiederholt, bis die Intervalllänge kleiner als die vorgegebene Genauigkeit ist: |b-a| < ε.
Etwas formaler:
1. Startwerte a, b und ε eingeben
2. Berechne
3. Falls f(a) · f(z) > 0 dann setze a = z sonst b = z
4. Falls |b-a| < ε dann Abbruch und Ausgabe der Nullstelle sonst zurück zu 2.
Zur Konvergenzgeschwindigkeit: Da wie erwähnt das Intervall bei jedem Schritt halbiert wird, gilt
Es besteht demnach eine logarithmische Abhängigkeit bezogen auf die Genauigkeit bzw. die Intervalllänge.
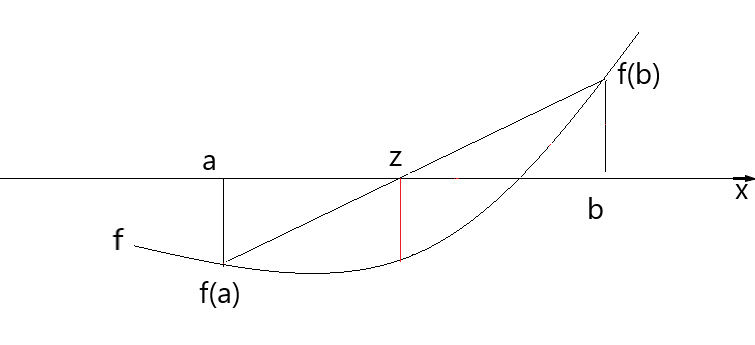
Auch bei diesem Verfahren benötigt man zwei Startwerte a und b, deren Funktionswerte f(a) und f(b) ein unterschiedliches Vorzeichen haben.
Im Unterschied zum Bisektionsverfahren ist hier die Nullstelle z der Sekante der nächste Näherungswert.
Die Sekante verläuft durch die Punkte ( a / f(a) ) und ( b / f(b) ) und lässt sich darstellen durch s(t) = m · x + b.
Die Steigung der Sekante beträgt .
Setzt man außerdem den ersten Startpunkt in die Sekantengleichung ein, ist b = f(a) - m · a. Die Sekantengleichung lautet demnach s(t) = m (x - a) + f(a). Es folgt für die Nullstelle .
Der zugehörige Algorithmus:
1. Startwerte a und b eingeben
2. Berechne
3. Falls f(a) · f(z) > 0 dann setze a = z sonst b = z
4. Falls Abbruchbedingung erfüllt, dann Ausgabe z sonst zurück zu 2.
Als etwas problematisch erweist sich die Abbruchbedingung. Man kann nicht einfach eine vorgegebene Genauigkeit ε verwenden, die die Differenz der beiden Intervallgrenzen berücksichtigt. Denn wenn im Intervall die Steigung der Funktion streng monoton ist (im Bild wächst sie stetig an), wird bei jedem Iteratiosschritt immer die gleiche Grenze (im Bild die linke) verändert. Die Intervalllänge ist mindestens so groß wie der Abstand der Nullstelle zur nicht veränderten Grenze (im Bild zu b) !
Weitere Abbruchkriterien können sein:
Differenz aufeinanderfolgender Näherungswerte mit einer unteren Schranke versehen.
Als Sicherung: Anzahl der möglichen Iterationsschritte begrenzen.
Um zumindest die Anzahl der störenden Fälle einer 'stehenbleibenden' Grenze zu verringern, wird Schritt 3 modifiziert:
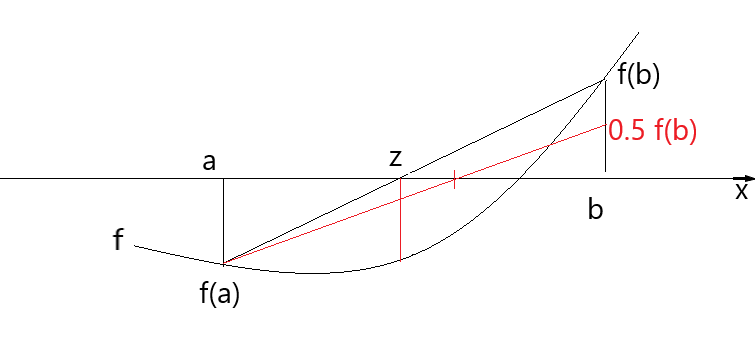
3. Falls f(a) · f(z) > 0 dann setze (a = z und verwende f(b)/2 statt f(b)) sonst b = z
Zur Berechnung des nächsten Näherungswertes wird ein geänderter Funktionswert der stehengebliebenen Grenze im nächsten Iterationsschritt herangezogen: statt f(b) wird k · f(b) verwendet mit 0 < k < 1. Im Beispiel ist k = 0.5. Durch diesen 'Kniff' rückt der zweite Punkt für eine erneute Sekantenberechnung näher an die x-Achse heran. Entweder erhält man eine verbesserte Näherung oder erreicht sogar einen Wechsel der zu ersetzenden Intervallgrenze.
Anmerkung: Das verbesserte Verfahren wird Illinois-VerfahrenMöglicher Ursprung dieser Veränderung ist die University of Illinois in den 1950er Jahren. genannt. In der nachfolgenden Berechnungen wird dieses Verfahren angewendet.
Zur Konvergenzgeschwindigkeit ist im Allgemeinen etwas besser als beim Bisektionsverfahren. Man spricht in diesem Fall von superlinearer Konvergenz.
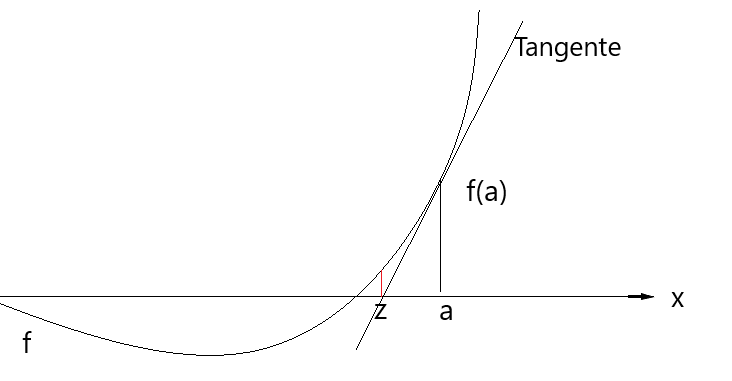
Für diesen Algorithmus benötigt man nur einen Startwert a. Es wird eine Tangente im Startpunkt an den Graphen der Funktion gelegt. Der nächste Näherungswert z ist die Nullstelle dieser Tangente,
Die Steigung m der Tangente an f im Punkt ( a / f(a) ) entspricht dem Funktionswert der Ableitungsfunktion f' an der Stelle a: m = f '(a).
Setzt man den Startpunkt und die Steigung in die Tangentengleichung ein (wie bei regula falsi), folgt für die Nullstelle der Tangente .
Der Algorithmus:
1. Startwert a und Genauigkeit ε eingeben
2. Setze z = a
3. Setze zalt = z
4. Berechne
5. Falls |z-zalt| < ε dann Abbruch und Ausgabe z sonst weiter bei 3.
Es sei angemerkt, dass an der einfachen Nullstelle der zweifach stetigen Funktion f die Steigung nicht Null betragen darf.
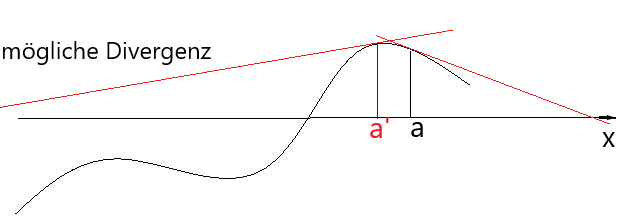
Der Startwert sollte hinreichend nahe an der Nullstelle liegen, denn es kann vom gewählten Startwert abhängen, ob das Newton-Verfahren sich überhaupt der Nullstelle annähert - also konvergiert -
oder etwa sich immer weiter entfernt - also divergiert. Insbesondere sollte im Intervall zwischen Nullstelle und Startwert kein Extremum liegen. Auch eine Wendestelle ist sehr problematisch (siehe Bild für die Startwerte a' und a).
Die Konvergenzgeschwindigkeit ist deutlich höher als bei den bisher genannten Verfahren. Sie wird als quadratisch bezeichnet, ist aber abhängig von der Funktion f.
Ohne Beweis sei hier angegeben , dass man bei Annäherung an eine Nullstelle höherer Ordnung das Verfahren verbessert, wenn man als Näherung verwendet. k ist die Ordnung der Nullstelle.
Beispielsweise liegt bei der Funktion f(x) = (x - 2)3 an der Stelle x = 2 eine dreifache Nullstelle vor.
Anmerkung: Das HeronGriechischer Mathematiker und Ingenieur, der im ägyptischen Alexandria lehrte. Er lebte vermutlich im 1. Jahrhundert n. Chr.-Verfahren zur Quadratwurzelberechnung einer positiven Zahl a entspricht dem Newton-Verfahren mit der Funktion f(x) = x2 - a.
Funktion f(x) =
| Bisektion/regula falsi | Newton | ||
|---|---|---|---|
| linke Grenze: | Startwert: | ||
| rechte Grenze: | |||
| Genauigkeit: | Genauigkeit: | ||