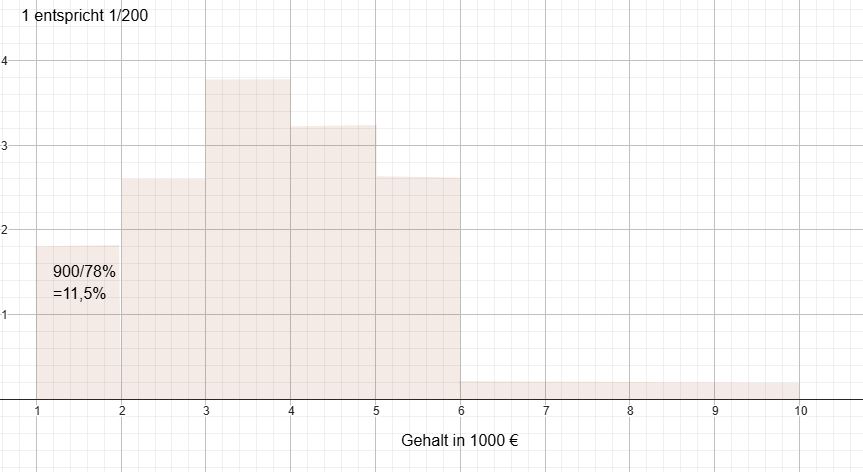
| Schüler | Disz I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Anna | 100 | 40 | 40 | 16 | 90 | 30 |
| Bertha | 73 | 80 | 39 | 14 | 50 | 51 |
| Clara | 46 | 72 | 49 | 10 | 40 | 60 |
| Doro | 10 | 64 | 46 | 30 | 75 | 48 |
a) Legen Sie anhand der erreichten Punkte eine Reihenfolge der Schülerleistungen fest.
b) Es soll ein anderer Bewertungsmaßstab eingeführt werden: Der Schüler mit den meisten Punkten bekommt eine „1“, der zweitbeste eine „2“ usw. Schreiben Sie obige Tabelle um, indem Sie die Noten eintragen. Legen Sie erneut eine Hierarchie fest.
c) Die erreichten Punktzahlen in einer Disziplin sollen linear gestreckt werden., d.h. der beste soll 100 Punkte bekommen, der schlechteste 0 Punkte. Dies wird erreicht mit der Transformation x → 100 ⋅ . Fertigen Sie erneut eine Tabelle an und legen Sie eine Reihenfolge fest.
| Schüler | Disz I | II | III | IV | V | VI | Aufg a) | Aufg b) | Aufg c) |
|---|---|---|---|---|---|---|---|---|---|
| Anna | 100 | 40 | 40 | 16 | 90 | 30 | 316 | 1+4+3+2+1+4 = 15 | 100+0+10+30+80+0 = 220 |
| Bertha | 73 | 80 | 39 | 14 | 50 | 51 | 307 | 2+1+4+3+3+2 = 15 | 70+100+0+20+20+70 = 280 |
| Clara | 46 | 72 | 49 | 10 | 40 | 60 | 277 | 3+2+1+4+4+1 = 15 | 40+80+100+0+0+100 = 320 |
| Doro | 10 | 64 | 46 | 30 | 75 | 48 | 273 | 4+3+2+1+2+3 = 15 | 0+60+70+100+70+60 = 360 |
Je nach Bewertungsmaßstab ändert sich die Reihenfolge der erzielten Punkte.
In a) : Anna - Bertha - Clara - Doro
In b) : alle gleich
In c) : Doro - Clara - Bertha - Anna
Je nach Bewertungsmaßstab ändert sich demnach die Reihenfolge in der Bestenliste. Dies ist sicher ein extremes Beispiel. Aber es zeigt:
Ein Ranking hängt auch vom Bewertungsmaßstab ab. Deshalb muss dieser Maßstab teil eines Rankings sein.
| Lokal | I | II | III | IV | V | VI |
|---|---|---|---|---|---|---|
| Entfernung in km (km-Stein) | 3 | 45 | 60 | 70 | 90 | 180 |
| Anzahl Anfahrten | 35 | 15 | 10 | 25 | 15 | 25 |
a) Die Transportkosten sind hoch. Wo muss Gonna ein Depot einrichten, um die Anzahl der gefahrenen Kilometer möglichst gering zu halten?
b) Die Standkosten für Lokal IV sind Gonna zu hoch. Sie will es schließen. Wo müsste nun das Depot eingerichtet werden?
Natürlich kann man den Graphen der Funktion f: Standort des Depots (km-Stein) -> gefahrene km erstellen, um das Minimum der gefahrenen km zu ermitteln.
Dann f(x) = 35 ⋅ |x - 3| + 15 ⋅ |x - 45| + 10 ⋅ |x - 60| + 25 ⋅ |x - 70| + 15 ⋅ |x - 90| + 25 ⋅ |x - 180|
Der Graph entspricht einem Polygonzug (abschnittsweise lineare Funktion). Beispielsweise entspricht einem Depot zwischen Lokal II und III
(also im Intervall I = [45,60] ) der Funktion f(x) = (x - 3) ⋅ 35 + (x - 45) &sdot 15 + (60 - x) ⋅ 10 + (70 - x) &sdot 25 + (90 - x) ⋅ 15 + (180 - x) ⋅ 25 = -25 ⋅ x + 7520
Für die anderen Intervalle entsprechend.
Besser: Man kann den Sachverhalt als Bestimmung des Minimums der mittleren linearen Abweichung auffassen. Das Minimum der mittleren linearen Abweichung ist der Median.
mittlere lin. Abweichung: ⋅ (35 ⋅ |3 - x| + 15 ⋅ |45 - x| + 10 ⋅ |60 - x| + 25 ⋅ |70 - x| + 15 ⋅ |90 - x| + 25 ⋅ |180 - x|)
Gesucht ist der Mittelwert xmed, für den diese Funktion minimal wird. Das Minimum der mittleren linearen Abweichung ist der Median.
Bei 125 Fahrten ist demnach der km-Wert der 63. Fahrt der Median (alle Fahrten sortiert in einer Reihe gelistet).
Bei km-Stein 70 ist demnach das Depot einzurichten.
zu b)
Fallen die Fahrten zu Lokal IV weg, sind noch 100 Fahrten zu absolvieren. Die Funktion f wird natürlich entsprechend modifiziert.
Nun ist der Median das arithmetische Mittel der 50. und 51. Anfahrt: = 52,5 km. Das Depot kann in diesem Fall irgendwo zwischen dem 2. und 3. Lokal liegen.
Es gibt nicht die 'eine' richtige Lösung, sondern man kann verschiedene vernünftige Ansätze wählen. Vorausgesetzt wird dabei eine fortlaufende Nummerierung (hier mit 1 beginnend).
Der Schätzwert sollte natürlich mindestens so hoch sein wie der höchste auftauchende Wert max ( = 90).
Demnach Schätzwert = max + Korrekturglied
Größen: größter Wert max = 90 ; kleinster Wert min = 5 ; Anzahl der Werte k = 5
Ideen:
1. max + min = 90 + 5 = 95 Fühlt sich etwas zu niedrig an
2. max + σ = 55 + ≈ 90 + 30 = 120 Fühlt sich etwas zu hoch an
3. Zu dem Maximum wird das arithmetische Mittel der Lücken addiert. Die Summe der Lücken zwischen den sortierten Werten beträgt: sl = 4 + 31 + 29 + 8 + 13 = 85 = max - k
Daraus resultiert der Mittelwert der Lücken: = = 17
Der Schätzwert ist dann max + = 90 + 17 = 107 ( = max + - 1)
Dieser Ansatz erscheint am besten geeignet.
Antwort zu Ansatz 3: Merle schätzt den Bestand auf 107 Taxis.
Bei Interesse: German-Tank-Problem von 1941: anhand von erbeuteten Panzern und deren Seiennummern wurde die monatliche Produktionsrate von
Panzern abgeschätzt; oder heutzutage wird anhand von Seriennummern bzw. IMEI-Nummern z.B. die Produktionsmenge von iPhones abgeschätzt. (Deshalb werden häufig Seriennummern nicht mehr fortlaufend vergeben.)
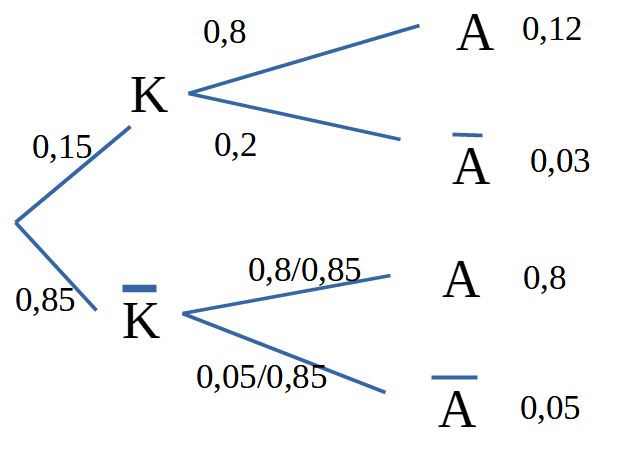
a) Erstellen Sie eine 6-Felder-Tafel.
b) Aus dem Urlaub kommt er mit einem Sonnenbrand wieder. Mit welcher Wahrscheinlichkeit war er an der See?
Ereignis U: Urlaubsort , Ereignis S: er bekommt einen Sonnenbrand
| S | S | ||
|---|---|---|---|
| Berge | 0.3⋅0.2 = 0.06 | 0.3⋅0.8 = 0.24 | 0.3 |
| Metropole | 0.2⋅0.1 = 0.02 | 0.2⋅0.9 = 0.18 | 0.2 |
| See | 0.5⋅0.3 = 0.15 | 0.5⋅0.7 = 0.35 | 0.5 |
| 0.23 | 0.77 | 1 |
zu b)
Es wird eine bedingte Wahrscheinlichkeit berechnet. Die Bedingung ist, einen Sonnenbrand zu besitzen.
PS(See) = = ≈ 0,65.
Er war unter der Bedingung, einen Sonnenbrand zu haben, etwa mit einer Wahrscheinlichkeit von 65% an der See.
Ereignis L: Location , Ereignis M: er trifft Manni
| M | M | ||
|---|---|---|---|
| Ma-Party | ⋅0.1 = | ⋅0.9 = | |
| Disco | ⋅0.6 = | ⋅0.4 = | |
| Döner-Bude | ⋅0.4 = | ⋅0.6 = | |
| 1 |
Es wird eine bedingte Wahrscheinlichkeit berechnet. Die Bedingung ist, Manni getroffen zu haben.
PM(Ma-Party) = = == .
Er war unter der Bedingung, Manni getroffen zu haben zu haben, etwa mit einer Wahrscheinlichkeit von 9% bei der Mathe-Party.
a) Mit welcher Wahrscheinlichkeit ist das 2. Kind ein Sohn?
b) Man weiß, die Familie hat (mindestens) einen Sohn. Mit welcher Wahrscheinlichkeit ist nun das 2. Kind ein Sohn?
zu a)
Die Ergebnismenge E bezogen auf die Kinder ist E = {(S,S) , (S,T) , (T,S) , (T,T)}. Jede Kinder-Kombination ist gleichwahrscheinlich.
Die Wahrscheinlichkeit,dass das 2. Kind ein Sohn ist, beträgt = 0,5.
zu b)
Die Ergebnismenge E lautet nun E = {(S,S) , (S,T) , (T,S)}, denn 2 Töchter kann es nicht geben.
Die Wahrscheinlichkeit,dass das 2. Kind ein Sohn ist, beträgt nun .
$$ \sum_{i=1}^{n} P(X=x_i) \cdot x_i$$ zum ersten Verfahren:
| xi | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| P(X=xi) |
Der Erwartungswert E(X) = ⋅ 1 + ⋅ 2 + ⋅ 3 + ⋅ 4 + ⋅ 5 =
zum zweiten Verfahren:
| xi | 2 | 3 |
|---|---|---|
| P(X=xi) |
Der Erwartungswert E(X) = ⋅ 2 + ⋅ 3 =
Das zweite Verfahren ist demnach vorzuziehen, denn der Erwartungswert ist kleiner. Im Mittel muss man weniger als drei Testungen durchführen, um das defekte Bauteil zu erkennen. Im ersten Verfahren sind es im Mittel über drei Testungen.
Anmerkung: Stehen nur noch zwei Bauteile zur Auswahl, reicht schon ein Test aus, um das defekte Teil zu lokalisieren.
| Augenzahl | 2 | 3 | 4 | 4 | 5 | 5 | 6 | 6 | 7 | 7 | 8 | 8 | 9 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| xi | -1 | 0 | 1 | -7 | 2 | -8 | 3 | -9 | 4 | -10 | 5 | -11 | 6 | -12 | 7 | 8 | 9 |
| P(X=xi) |
Der Erwartungswert E(X) = ⋅ (-1) + ⋅ 0 + ... + ⋅ 9 = 0
Ein Spiel ist fair, wenn der Erwartungswert 0 ist. Das ist hier der Fall.
Die Wahrscheinlichkeitsverteilung von X:
| xi | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| P(X=xi) | ⋅0,44= | ⋅0,6⋅0,43= | ⋅0,62⋅0,42= | ⋅0,63⋅0,4= | ⋅0,64= |
Erwartungswert E(X) , Varianz V(X) und Standardabweichung σ = $$ E(X) = \mu = \sum_{i=1}^{n} P(X=x_i) \cdot x_i = \frac {16}{625} \cdot 0 + \frac {96}{625} \cdot 1 + \frac {216}{625} \cdot 2 + \frac {216}{625} \cdot 3 + \frac {81}{625} \cdot 4 = \frac {1500}{625} = \frac {12}{5}$$ $$ V(X) = \sum_{i=1}^{n} P(X=x_i) \cdot {(x_i - \mu)}^2 = \frac {16}{625} \cdot \frac {144}{25} + \frac {96}{625} \cdot \frac {49}{25} + \frac {216}{625} \cdot \frac {4}{25} + \frac {216}{625} \cdot \frac {9}{25} + \frac {81}{625} \cdot \frac {64}{25} = \frac {15000}{15625} = \frac {24}{25}$$ $$ Standardabweichung ~\sigma = \sqrt {V(X)} = \frac {1}{5} \cdot \sqrt {24} = \frac {2}{5} \cdot \sqrt {6} \approx 0,98 $$
b) Geben Sie die Wahrscheinlichkeit dafür an, dass von den 21 Schülern der Klasse (mindestens) zwei am gleichen Tag Geburtstag haben.
Da nichts weiter über die Verteilung der Zufallsvariablen X bekannt ist (hier: Anzahl der Taschen mit bestimmter Länge), kann nur die Tschebyscheff-Ungleichung herangezogen werden.
Tschebyscheff: Für die Wahrscheinlichkeit, daß die Zufallsvariable X einen Wert annimmt, der um mindestens c vom Erwartungswert abweicht, gilt P(|X - σ| ≥ c) ≤ .
Die Abweichung (in Zoll) beträgt hier c = 0,24 = 2 ⋅ σ.
Dann gilt: P(|X - 6| ≥ 0,24) ≤ = .
Er muss mit höchstens 25% Ausschuss rechnen.
zu b)
Die Idee: Es wird die Gegenwahrscheinlichkeit berechnet: alle Schüler haben an verschiedenen Tagen Geburtstag.
Man nehme einen (beliebigen) Schüler, der an einem bestimmten Tag Geburtstag hat. Ein (beliebiger) zweiter Schüler hat mit der Wahrscheinlichkeit an diesem Tag nicht Geburtstag. Ein (beliebiger) dritter Schüler hat mit der Wahrscheinlichkeit an beiden Geburtstagen nicht selbst Geburtstag usw.
Die Wahrscheinlichkeit P, dass n Schüler an jeweils verschiedenen Tagen Geburtstag haben, ist $$P = \prod_{i=0}^{n-1} \frac {365 - i}{365} = \frac {365 \cdot 364 \cdot ... \cdot (365-n+1)} {365^n}$$ Für n = 21 gilt $$P = \prod_{i=0}^{20} \frac {365 - i}{365} = \frac {365 \cdot 364 \cdot ... \cdot 345} {365^{21}} \approx 0,56 $$ Die Wahrscheinlichkeit, dass mindestens zwei Schüler am gleichen Tag Geburtstag haben, beträgt dann 1 - 0,56. Das entspricht 44%.
Seine 30% Siegchancen beziehen sich auf 100%. Fallen nun die 40% von Bolt weg, betragen seine Siegchancen nicht mehr , sondern = 50%.
Entsprechend betragen die Siegchancen von Asafa Powell ≈ 16,7%.
a) Musste Anastasia bei der Umfrage bezüglich eines repräsentativen Ergebnisses etwas beachten?
b) Stellen Sie eine Vier-Felder Tafel auf.
c) Sind die Merkmale Geschlecht und Begeisterung für Mathematik unabhängig?
Die Schüler müssen repräsentativ zufällig ausgewählt werden, also über alle Altersstufen und Klassen und Geschlecht, und nicht etwa nur unter Profilfach-Mathematik-Schülern.
zu b)
Ereignis W: Schüler ist weiblich , Ereignis B: Schüler begeistert sich für Mathematik
Gegeben: P(W) = = 0,56 , PW(B) = 0,6 sowie PB(W) = 0,44
Es gilt: P(B ∩ W) = PW(B) ⋅ P(W) = 0,6 ⋅ 0,56 = 0,336
weiter: P(B) = P(W ∩ B) + P(W ∩ B) = (0,56 - 0,336) + P(B) ⋅ PB(W) = 0,224 + P(B) ⋅ 0,44
Und daraus P(B) = 0,4
| W | W | ||
| B | 0,336 (42) | 0,264 (33) | 0,6 (75) |
| B | 0,224 (28) | 0,176 (22) | 0,4 (50) |
| 0,56 (70) | 0,44 (55) | 1 |
In Klammern ist die Anzahl der Schüler angegeben.
zu c)
Die Ereignisse W und B sind unabhängig, falls gilt: P(W∩B) = P(W) ⋅ P(B)
P(W∩B) = 0,336 und P(W) ⋅ P(B) = 0,56 ⋅ 0,6 = 0,336 → Die Ereignisse sind unabhängig.
Alternativ: W und B sind unabhängig, falls PW(B) = P(B) ist.
Die Wahrscheinlichkeiten sind jeweils 0,6 → Unabhängigkeit von W und B
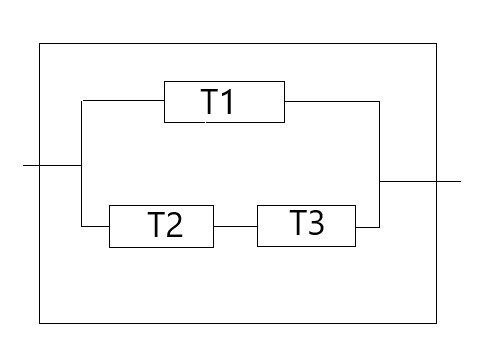 Sie sind gemäß der Zeichnung zusammengeschaltet. Mit welcher Zuverlässigkeit fließt Wasser durch die Konstruktion?
Sie sind gemäß der Zeichnung zusammengeschaltet. Mit welcher Zuverlässigkeit fließt Wasser durch die Konstruktion?Ersatzschaltbild: Die Pumpen T1 und T23 sind parallel geschaltet. Durch die gesamte Maschine fließt Wasser, falls mindestens eine der beiden Pumpen T1 und T23 arbeitet. Man berechnet die Gegenwahrscheinlichkeit: beide arbeiten nicht mit der Wahrscheinlichkeit 0,1 ⋅ 0,6 = 0,06.
Also fließt mit der Wahrscheinlichkeit 0,94 Wasser durch die Konstruktion.
a) Vater und Mutter haben den Genotyp Bb. Welchen Genotyp kann das Kind haben? Mit welchen Wahrscheinlichkeiten treten die möglichen Ereignisse ein?
b) Das Kind Paul hat den Genotyp bb. Welche Elternkombinationen sind denkbar? Berechnen Sie für jede denkbare Elternkombination die Wahrscheinlichkeit, mit der beim Kind der Genotyp bb auftritt.
c) Die Genotypen der Eltern werden unabhängig voneinander gemäß der oben angegebenen Verteilung ausgelost. Pauls Freundin Anna wird zum ersten Mal zu seinen Eltern eingeladen. Sie will sich gut auf das Gespräch vorbereiten durch Besuch der Club-Fan-Seiten. Mit welcher Wahrscheinlichkeit wird sie auf Fußball angesprochen – wenn also mindestens ein Elternteil aktiver Fußballfan ist?

Möglich sind die Genotypen bb, Bb sowie BB. (Anmerkung: bB und Bb sind gleich.)
Vater und Mutter vererben die jeweiligen Allele zu je 0,5.
Daraus folgt: P(bb) = 0,25 ; P(bB) = 0,5 , P(BB) = 0,25
zu b)
Die Eltern können beide die Genotypen bb besitzen, beide Bb oder eine Kombination aus Bb und bb.
Besitzen beide Elternteile den Genotyp bb, hat das Kind zu 100% den Genotyp bb.
Besitzen beide Elternteile den Genotyp Bb, hat das Kind zu 25% den Genotyp bb (s. Aufgabe a).
Bei einer Kombination aus Bb und bb hat das Kind zu 50% (entspricht 0,5 ⋅ 1 = 0,5 im Baumdiagramm) den Genotyp bb.
zu c)
Die Wahrscheinlichkeit, dass ein Elternteil Fußballfan ist, beträgt 0,4 = ( 0,3 + 0,1).
Die Wahrscheinlichkeit, dass beide Elternteile keine Fußballfans sind, beträgt 0,36 (= 0,6 ⋅ 0,6).
Sie wird mit einer Wahrscheinlichkeit von 0,64 auf Fußball angesprochen.
Gesucht ist die Eintrittswahrscheinlichkeit p für die Genehmigung der Klausur.
Da die Wette fair sein soll, gilt: E(X) = 0.
Dann gilt: E(X) = p ⋅ 8 + (1 - p) ⋅ (-10) = 0 → p = ≈ 0,556
Mit einer Wahrscheinlichkeit von fast 56% muss die Klausur genehmigt werden.
a) Ermitteln Sie den Erwartungswert für die Anzahl der durchzuführenden Sätze.
b) Wettprofi W. bietet an, 8 € auszuzahlen bei einem Einsatz von 5 €, wenn fünf Sätze notwendig sind. Ansonsten ist der Einsatz verloren. Ist das Spiel fair? Geben Sie ggfs. eine Auszahlungsquote an, damit die Wette fair ist.
Die Zufallsvariable X gibt die Anzahl der durchzuführenden Sätze an.. Sie kann die Werte 3, 4 oder 5 annehmen.
Wenn nur drei Sätze gespielt werden, muss eine Mannschaft dreimal hintereinander gewinnen. Die Wahrscheinlichkeit dafür beträgt 0,53 = . Das gilt für jede Mannschaft. Insgesamt ist P(X=3) = 0,25 = .
Wenn 4 Sätze gespielt werden, gewinnt eine Mannschaft dreimal und verliert einmal. Der Verlust kann im ersten, zweiten, dritten aber nicht im vierten Spiel geschehen. Die Wahrscheinlichkeit beträgt demnach 3 ⋅ 0,53 ⋅ 0,5 = . Das gilt für jede Mannschaft. Insgesamt ist P(X=4) = 2 ⋅ = .
Die Wahrscheinlichkeit für 5 Sätze beträgt dann ebenfalls P(X=5) = ( = 1 - - ).
Für das Spielen von 5 Sätzen kann auch überlegt werden, dass man 4 Sätze spielen muss, von denen jeweils zwei von einer Mannschaft gewonnen werden. Das fünfte Spiel ist dann egal.
Es gibt = 6 Möglichkeiten dafür. Insgesamt 6 ⋅ 0,54 =
| xi | 3 | 3 | 5 |
| P(X=xi) |
zu b)
Sei Y die Zufallsvariable, die den Gewinn in € angibt. Es gilt:
| yi | -5 | 3 |
| P(Y=yi) |
Gesucht: E(Y) = (-5) ⋅ + 3 ⋅ = -2.
Das Spiel ist nicht fair. Man verliert im Durchschnitt bei jeder Wette 2 €.
Damit die Wette fair ist, muss gelten: E(Y) = 0.
a sei der Gewinn in €, falls 5 Sätze gespielt werden.
E(Y) = (-5) ⋅ + a ⋅ = 0 → a = = 8
Der Wettprofi müsste für eine faire Wette bei 5 Spielsätzen 13 € auszahlen.