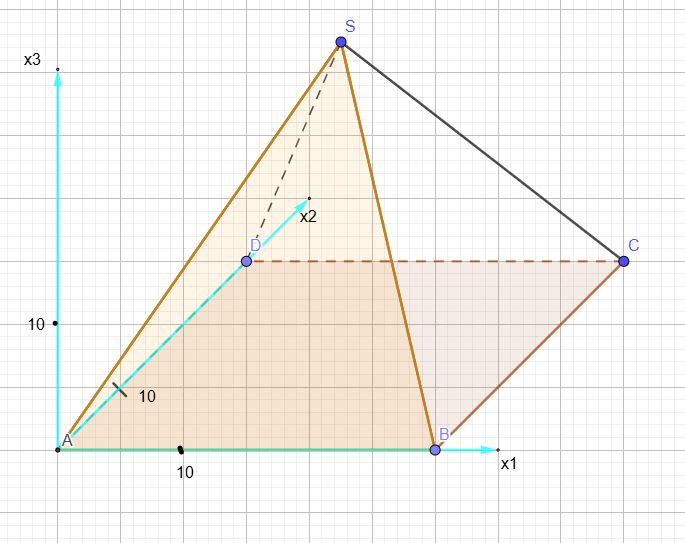
a) Geben Sie die Gerade g durch die Punkte A und B an.
b) Bestimmen Sie einen weiteren Punkt auf der Geraden g und zeigen Sie, dass C nicht auf der Geraden liegt.
c) Wie lautet die Gerade g’, die parallel zu g ist und durch C verläuft?
d) Ermitteln Sie den Winkel zwischen den Vektoren \( \vec{AB}\) und \( \vec{AC}\).
zu a)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu b)
weiterer Punkt E: z.B. λ = -1 setzen.
Dann: \( \vec{e}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~(-1) \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} ~=~ \begin{pmatrix} 1 \\ 1 \\ 6 \end{pmatrix}\)\(~~\rightarrow~~E(1/1/6) \)
zu c)
Parallele Geraden besitzen kollineare Richtungsvektoren.
g': \( \vec{r}~=~ \begin{pmatrix} 1 \\ -1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu d)
Mit Skalarprodukt: \( \vec{AB} \cdot \vec{AC} = | \vec{AB}| \cdot | \vec{AC} | \cdot cos \alpha ~~mit~~\alpha=\angle (\vec{AB},\vec{AC}) \)
dann: \(\alpha~=~arccos\frac {\vec{AB} \cdot \vec{AC}}{| \vec{AB}| \cdot | \vec{AC} |}\)\( ~=~arccos\frac{\begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \cdot \begin{pmatrix} -1 \\ -2 \\ 0 \end{pmatrix}}{\sqrt{10}\cdot\sqrt{5}}~=~arccos\frac{-1}{\sqrt{50}}~\approx~98,1^\circ\)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu b)
weiterer Punkt E: z.B. λ = -1 setzen.
Dann: \( \vec{e}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~(-1) \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} ~=~ \begin{pmatrix} 1 \\ 1 \\ 6 \end{pmatrix}\)\(~~\rightarrow~~E(1/1/6) \)
zu c)
Parallele Geraden besitzen kollineare Richtungsvektoren.
g': \( \vec{r}~=~ \begin{pmatrix} 1 \\ -1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu d)
Mit Skalarprodukt: \( \vec{AB} \cdot \vec{AC} = | \vec{AB}| \cdot | \vec{AC} | \cdot cos \alpha ~~mit~~\alpha=\angle (\vec{AB},\vec{AC}) \)
dann: \(\alpha~=~arccos\frac {\vec{AB} \cdot \vec{AC}}{| \vec{AB}| \cdot | \vec{AC} |}\)\( ~=~arccos\frac{\begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \cdot \begin{pmatrix} -1 \\ -2 \\ 0 \end{pmatrix}}{\sqrt{10}\cdot\sqrt{5}}~=~arccos\frac{-1}{\sqrt{50}}~\approx~98,1^\circ\)
a) Zeichnen Sie das Vierflach.
b) Bestimmen Sie die Grundebene E (also die Ebene durch die Punkte A, B und C) in Normalenform und geben Sie den Abstand der Spitze S von der Grundfläche an. (mögliche Lösung für E: 2x1-3x3+3=0)
c) Ermitteln Sie den Fußpunkt F des Lotes von S auf die Grundebene E. Liegt F innerhalb des Dreiecks ABC?
d) Geben Sie den Winkel zwischen der Grundfläche und der Geraden durch die Punkte A und S an.
e) Berechnen Sie den Spiegelpunkt S’ des Punktes S an der Grundebene.
f) Geben Sie den Flächeninhalt des Dreiecks ABC an sowie den Rauminhalt des Vierflachs.
zu a) 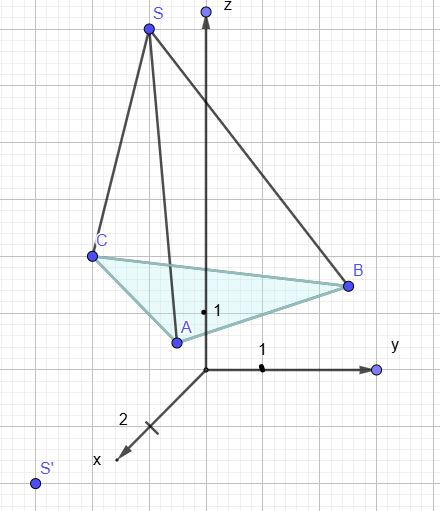
Anmerkung: Der Punkt A befindet sich (alle drei Koordinaten sind negativ) 'hinter' allen drei Grundebenen und 'schwebt' nicht etwa über der x-y-Grundebene.
zu b)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}= \begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: 2x1 - 3x3 + 3 = 0
zu c)
Rechenweg: Zu E orthogonale Gerade g durch S angeben; Schnittpunkt von g und E ist der Lotfußpunkt F.
Der Richtungsvektor von g ist kollinear zum Normalenvektor von E:
Also g: \(\vec{r}= \begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + \lambda \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\)
Nun g in die Normalenform von E einsetzen:
\(\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\cdot \left(\begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + \lambda \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}- \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix}\right)=0\) \(~\rightarrow~-16+13\lambda+3=0\) \(~\rightarrow ~\lambda=1\)
λ in g einsetzen:
\(\vec{f}= \begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + 1\cdot \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\) \(~\rightarrow~F(6/1/5)\) (*)
F liegt in E, deshalb existieren λ und μ mit
\( \vec{f}~=~ \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\)
F liegt innerhalb der Grundfläche ABC, falls 0 < λ < 1 und 0 < μ < 1 sowie λ + μ < 1 gilt.
Hier sieht man sofort: F entspricht dem Randpunkt C der Grundfläche.
allgemeine Lösung:
Aus (*) folgt:
6 = -3 + 6λ + 9μ
1 = -2 + 6λ + 3μ → λ = 0 , μ = 1
5 = -1 + 4λ + 6μ
Anmerkung: Überprüfung der 3. Gleichung nicht vergessen!
zu d)
Um den Winkel α zwischen der Ebene E und der Geraden \(\vec{AS}\) zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix}\right|}{\sqrt{13}\cdot\sqrt{139}}~=~arccos\frac{13}{\sqrt{1807}}~\approx~72,2^\circ\)
Der Winkel zwischen der Geraden AS und der Grundebene E beträgt α ≈ 17,8°.
zu e)
Um zum Punkt S' zu gelangen, wird vom Lotfußpunkt F (bzw. in diesem Fall Punkt C) der Vektor \(\vec{SF}\) angelegt:
\(\vec{s'}=\vec{f}+\vec{SF}=\begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix}+\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}=\begin{pmatrix} 8 \\ 1 \\ 2\end{pmatrix}\)
Der Spiegelpunkt S' zu S bzgl. der Ebene E ist S'(8/1/2).
zu f)
Der Flächeninhalt A des Dreiecks ABC kann mit dem Vektorprodukt berechnet werden:
AABC = \(\frac{1}{2}\left|\vec{AB}\times\vec{AC}\right|\)\(=\frac{1}{2}\left|\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\right|= \frac{1}{2}\left|\begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix} \right|\)\(=\frac{1}{2}\sqrt{1872}\approx21,6~FE\)
Das Volumen des Vierflachs ABCS kann mit dem Spatprodukt ermittelt werden:
VABCS = \(\frac{1}{6}\left|(\vec{AB}\times\vec{AC})\cdot\vec{AS}\right|\)\(=\frac{1}{6}\left|\left(\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\right)\cdot\begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix} \right|\)\(= \frac{1}{6}\left|\begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix}\cdot \begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix} \right|=\frac{1}{6}\cdot 156 = 26~ VE\)
Das Volumen des Vierflachs beträgt 26 VE.

Anmerkung: Der Punkt A befindet sich (alle drei Koordinaten sind negativ) 'hinter' allen drei Grundebenen und 'schwebt' nicht etwa über der x-y-Grundebene.
zu b)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}= \begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: 2x1 - 3x3 + 3 = 0
zu c)
Rechenweg: Zu E orthogonale Gerade g durch S angeben; Schnittpunkt von g und E ist der Lotfußpunkt F.
Der Richtungsvektor von g ist kollinear zum Normalenvektor von E:
Also g: \(\vec{r}= \begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + \lambda \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\)
Nun g in die Normalenform von E einsetzen:
\(\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\cdot \left(\begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + \lambda \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}- \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix}\right)=0\) \(~\rightarrow~-16+13\lambda+3=0\) \(~\rightarrow ~\lambda=1\)
λ in g einsetzen:
\(\vec{f}= \begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} + 1\cdot \begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}\) \(~\rightarrow~F(6/1/5)\) (*)
F liegt in E, deshalb existieren λ und μ mit
\( \vec{f}~=~ \begin{pmatrix} -3 \\ -2 \\ -1 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\)
F liegt innerhalb der Grundfläche ABC, falls 0 < λ < 1 und 0 < μ < 1 sowie λ + μ < 1 gilt.
Hier sieht man sofort: F entspricht dem Randpunkt C der Grundfläche.
allgemeine Lösung:
Aus (*) folgt:
6 = -3 + 6λ + 9μ
1 = -2 + 6λ + 3μ → λ = 0 , μ = 1
5 = -1 + 4λ + 6μ
Anmerkung: Überprüfung der 3. Gleichung nicht vergessen!
zu d)
Um den Winkel α zwischen der Ebene E und der Geraden \(\vec{AS}\) zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix} \cdot \begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix}\right|}{\sqrt{13}\cdot\sqrt{139}}~=~arccos\frac{13}{\sqrt{1807}}~\approx~72,2^\circ\)
Der Winkel zwischen der Geraden AS und der Grundebene E beträgt α ≈ 17,8°.
zu e)
Um zum Punkt S' zu gelangen, wird vom Lotfußpunkt F (bzw. in diesem Fall Punkt C) der Vektor \(\vec{SF}\) angelegt:
\(\vec{s'}=\vec{f}+\vec{SF}=\begin{pmatrix} 6 \\ 1 \\ 5 \end{pmatrix}+\begin{pmatrix} 2 \\ 0 \\ -3 \end{pmatrix}=\begin{pmatrix} 8 \\ 1 \\ 2\end{pmatrix}\)
Der Spiegelpunkt S' zu S bzgl. der Ebene E ist S'(8/1/2).
zu f)
Der Flächeninhalt A des Dreiecks ABC kann mit dem Vektorprodukt berechnet werden:
AABC = \(\frac{1}{2}\left|\vec{AB}\times\vec{AC}\right|\)\(=\frac{1}{2}\left|\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\right|= \frac{1}{2}\left|\begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix} \right|\)\(=\frac{1}{2}\sqrt{1872}\approx21,6~FE\)
Das Volumen des Vierflachs ABCS kann mit dem Spatprodukt ermittelt werden:
VABCS = \(\frac{1}{6}\left|(\vec{AB}\times\vec{AC})\cdot\vec{AS}\right|\)\(=\frac{1}{6}\left|\left(\begin{pmatrix} 6 \\ 6 \\ 4 \end{pmatrix} \times \begin{pmatrix} 9 \\ 3 \\ 6 \end{pmatrix}\right)\cdot\begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix} \right|\)\(= \frac{1}{6}\left|\begin{pmatrix} 24 \\ 0 \\ -36 \end{pmatrix}\cdot \begin{pmatrix} 7 \\ 3 \\ 9 \end{pmatrix} \right|=\frac{1}{6}\cdot 156 = 26~ VE\)
Das Volumen des Vierflachs beträgt 26 VE.
a) Berechnen Sie den Abstand des Punktes D(6/17/13) von E sowie den Fußpunkt F des Lotes von D auf E.
b) Bestimmen Sie den Winkel zwischen g und E.
c) Ermitteln Sie die Punkte R und S auf der z-Achse so, dass die Dreiecke ABR und ABS bei R bzw. S einen rechten Winkel bilden.
zu a)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{p}~+~\lambda\cdot(\vec{q}-\vec{p})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} -1 \\ 4 \\ 6 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ 0 \\ -3 \end{pmatrix} \)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 8 \\ 2 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} -4 \\ -8 \\ -2 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 6 \\ 8 \\ 2 \end{pmatrix} \times \begin{pmatrix} -4 \\ -8 \\ -2 \end{pmatrix}= \begin{pmatrix} 0 \\ 4 \\ -16 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: x2 - 4x3 + 18 = 0
Um den Abstand d eines Punktes von einer Ebene zu bestimmen, wird der Punkt in die Hesseform der Ebenengleichung eingesetzt.
d(D,E) = \( \frac{1}{\sqrt{17}} \left| \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot\begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} + 18 \right| = \frac{1}{\sqrt{17}} \left|-35+18 \right| \)\( = \frac {17}{\sqrt{17}} \approx 4,1\)
Der Abstand des Punktes D von der Ebene E beträgt etwa 4,1 LE.
Um den Fußpunkt F zu ermitteln, wird der Schnittpunkt der zu E orthogonalen Geraden h durch D und der Ebene E bestimmt:
Gerade h: \( \vec{r}~=~ \begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} \)
h in E: \(\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot \left(\begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} + \lambda \begin{pmatrix} 0 \\ 1 \\ -4\end{pmatrix}\right)+18=0\) \(~\rightarrow~-35+17\cdot\lambda+18=0\) \(~\rightarrow ~\lambda=\frac{-17}{17}=-1\)
Nun λ in h einsetzen:
\( \vec{r}~=~ \begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} ~+~- 1 \cdot \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} ~=~\begin{pmatrix} 6 \\ 16 \\ 17 \end{pmatrix}\)
Der Lotfußpunkt von D bzgl der Ebene E ist F(6/16/17).
zu b)
Um den Winkel α zwischen der Ebene E und der Geraden g zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 0 \\ -3 \end{pmatrix}\right|}{\sqrt{17}\cdot\sqrt{18}}~=~arccos\frac{12}{\sqrt{306}}~\approx~46,7^\circ\)
Der Winkel zwischen der Geraden g und der Grundebene E beträgt α ≈ 43,3°.
zu c)
Zwei Vektoren sind genau dann orthogonal zueinander, wenn das Skalarprodukt Null ergibt.
Sei R ein Punkt auf der z-Achse, dann sind seine x- und y- Koordinaten Null.
Daraus ergeben sich 3 Bedingungen:
xR = yR = 0 sowie \(\vec{RA}\cdot\vec{RB} = 0\). Weiter:
\(\vec{RA}=\vec{a}-\vec{r}=\begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}=\begin{pmatrix} -6 \\ -2 \\ 4-z \end{pmatrix}\)
\(\vec{RB}=\vec{b}-\vec{r}=\begin{pmatrix} 0 \\ 6 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}=\begin{pmatrix} 0 \\ 6 \\ 6-z \end{pmatrix}\)
Mit \(\vec{RA}\cdot\vec{RB} = \begin{pmatrix} -6 \\ -2 \\ 4-z \end{pmatrix}\cdot\begin{pmatrix} 0 \\ 6 \\ 6-z \end{pmatrix}\)\(=0-12 + (4-z)\cdot(6-z)=z^2-10z+12=0\)\(\rightarrow z_1=5-\sqrt{13} ~und~z_2=5+\sqrt{13}\)
Demnach sind die gesuchten Punkte: R(0/0/5-\(\sqrt{13}\)) und S(0/0/5+\(\sqrt{13}\)).
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{p}~+~\lambda\cdot(\vec{q}-\vec{p})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} -1 \\ 4 \\ 6 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ 0 \\ -3 \end{pmatrix} \)
Ebene E in Punktrichtungsform:
E: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~+~\mu\cdot(\vec{c}-\vec{a})~~\)
E: \(\vec{r}~=~\begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 6 \\ 8 \\ 2 \end{pmatrix}~+~\mu \cdot \begin{pmatrix} -4 \\ -8 \\ -2 \end{pmatrix}\)
Ebene E in Normalenform: \(\vec{n}\cdot (\vec{r}-\vec{a})=0 \) mit
Normalenvektor \(\vec{n'}=\begin{pmatrix} 6 \\ 8 \\ 2 \end{pmatrix} \times \begin{pmatrix} -4 \\ -8 \\ -2 \end{pmatrix}= \begin{pmatrix} 0 \\ 4 \\ -16 \end{pmatrix} \)\(~\rightarrow~\vec{n}=\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\)
Und daraus E: \(\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot \left(\vec{r}- \begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix}\right)=0\)
oder in Koordinatenform E: x2 - 4x3 + 18 = 0
Um den Abstand d eines Punktes von einer Ebene zu bestimmen, wird der Punkt in die Hesseform der Ebenengleichung eingesetzt.
d(D,E) = \( \frac{1}{\sqrt{17}} \left| \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot\begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} + 18 \right| = \frac{1}{\sqrt{17}} \left|-35+18 \right| \)\( = \frac {17}{\sqrt{17}} \approx 4,1\)
Der Abstand des Punktes D von der Ebene E beträgt etwa 4,1 LE.
Um den Fußpunkt F zu ermitteln, wird der Schnittpunkt der zu E orthogonalen Geraden h durch D und der Ebene E bestimmt:
Gerade h: \( \vec{r}~=~ \begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} \)
h in E: \(\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix}\cdot \left(\begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} + \lambda \begin{pmatrix} 0 \\ 1 \\ -4\end{pmatrix}\right)+18=0\) \(~\rightarrow~-35+17\cdot\lambda+18=0\) \(~\rightarrow ~\lambda=\frac{-17}{17}=-1\)
Nun λ in h einsetzen:
\( \vec{r}~=~ \begin{pmatrix} 6 \\ 17 \\ 13 \end{pmatrix} ~+~- 1 \cdot \begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} ~=~\begin{pmatrix} 6 \\ 16 \\ 17 \end{pmatrix}\)
Der Lotfußpunkt von D bzgl der Ebene E ist F(6/16/17).
zu b)
Um den Winkel α zwischen der Ebene E und der Geraden g zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 0 \\ 1 \\ -4 \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 0 \\ -3 \end{pmatrix}\right|}{\sqrt{17}\cdot\sqrt{18}}~=~arccos\frac{12}{\sqrt{306}}~\approx~46,7^\circ\)
Der Winkel zwischen der Geraden g und der Grundebene E beträgt α ≈ 43,3°.
zu c)
Zwei Vektoren sind genau dann orthogonal zueinander, wenn das Skalarprodukt Null ergibt.
Sei R ein Punkt auf der z-Achse, dann sind seine x- und y- Koordinaten Null.
Daraus ergeben sich 3 Bedingungen:
xR = yR = 0 sowie \(\vec{RA}\cdot\vec{RB} = 0\). Weiter:
\(\vec{RA}=\vec{a}-\vec{r}=\begin{pmatrix} -6 \\ -2 \\ 4 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}=\begin{pmatrix} -6 \\ -2 \\ 4-z \end{pmatrix}\)
\(\vec{RB}=\vec{b}-\vec{r}=\begin{pmatrix} 0 \\ 6 \\ 6 \end{pmatrix} - \begin{pmatrix} 0 \\ 0 \\ z \end{pmatrix}=\begin{pmatrix} 0 \\ 6 \\ 6-z \end{pmatrix}\)
Mit \(\vec{RA}\cdot\vec{RB} = \begin{pmatrix} -6 \\ -2 \\ 4-z \end{pmatrix}\cdot\begin{pmatrix} 0 \\ 6 \\ 6-z \end{pmatrix}\)\(=0-12 + (4-z)\cdot(6-z)=z^2-10z+12=0\)\(\rightarrow z_1=5-\sqrt{13} ~und~z_2=5+\sqrt{13}\)
Demnach sind die gesuchten Punkte: R(0/0/5-\(\sqrt{13}\)) und S(0/0/5+\(\sqrt{13}\)).
a) Ermitteln Sie die gegenseitige Lage von g und E und bestimmen Sie gegebenenfalls ihren Schnittpunkt oder ihren Abstand.
b) Fällen Sie das Lot vom Punkt C(1/4/-2) auf die Ebene E und geben Sie den Lotfußpunkt F an. Welchen Abstand besitzt C von E? Ermitteln Sie den Spiegelpunkt C’ von C an der Ebene E.
c) Bestimmen Sie den Punkt D so, dass das Viereck ABCD ein Parallelogramm ergibt.
d) Sei die Gerade k gegeben durch die Punkte M (1/1/1) und N(2/-1/1). Bestimmen Sie den Abstand der Geraden g und k sowie die jeweiligen Lotfußpunkte.
zu a)
Mit 2-Punkte-Form: Gerade g: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~\)\(~\rightarrow~~\vec{r}~=~\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix} \)
Im R3 kann die Gerade g in E liegen oder parallel zu E sein oder sie besitzen einen Schnittpunkt.
Es gibt verschiedene Strategien, um die gegenseitige Lage zu bestimmen. Da E in Koordinatenform (und damit quasi in Normalenform) vorliegt, prüft man am einfachsten, ob ein Schnittpunkt vorliegt. Dazu setzt man g in E ein:
g in E: \(\begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix}\cdot \left(\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} + \lambda \begin{pmatrix} 4 \\ 1 \\ 0\end{pmatrix}\right)+65=0\) \(~\rightarrow~44+0\cdot\lambda+65=0\) \(~\rightarrow ~Widerspruch\) → g || E.
Nun soll der Abstand d von g und E bestimmt werden. Es genügt, den Abstand eines Punktes von g zu E zu bestimmen.
Es wird der Punkt A in die Hesseform der Ebenengleichung eingesetzt:
d(g,E) = d(A,E) = \( \frac{1}{\sqrt{66}} \left| \begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix}\cdot\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} + 65 \right| = \frac{1}{\sqrt{66}} \left|44 + 65 \right| \)\( = \frac {109}{\sqrt{66}} \approx 13,4\)
Die Gerade g und die Ebene E sind parallel zueinander. Ihr Abstand beträgt etwa 13,4 LE.
zu b)
Um den Abstand d eines Punktes von einer Ebene zu bestimmen, wird der Punkt in die Hesseform der Ebenengleichung eingesetzt.
d(C,E) = \( \frac{1}{\sqrt{66}} \left| \begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix}\cdot\begin{pmatrix} 1 \\ 4 \\ -2 \end{pmatrix} + 65 \right| = \frac{1}{\sqrt{66}} \left|1+65 \right| \)\( = \frac {66}{\sqrt{66}} \approx 8,1\)
Der Abstand des Punktes C von der Ebene E beträgt etwa 8,1 LE.
Um den Fußpunkt F zu ermitteln, wird der Schnittpunkt der zu E orthogonalen Geraden h durch C und der Ebene E bestimmt:
Gerade h: \( \vec{r}~=~ \begin{pmatrix} 1 \\ 4 \\ -2 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix} \)
h in E: \(\begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix}\cdot \left(\begin{pmatrix} 1 \\ 4 \\ -2 \end{pmatrix} + \lambda \begin{pmatrix} -1 \\ 4 \\ 7\end{pmatrix}\right)+65=0\) \(~\rightarrow~1+66\cdot\lambda+65=0\) \(~\rightarrow ~\lambda=\frac{66}{66}=1\)
Nun λ in h einsetzen:
\( \vec{r}~=~ \begin{pmatrix} 1 \\ 4 \\ -2 \end{pmatrix} ~+ ~ 1 \cdot \begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix} ~=~\begin{pmatrix} 0 \\ 8 \\ 5 \end{pmatrix}\)
Der Lotfußpunkt F von C bzgl der Ebene E ist F(0/8/5).
Alternativ kann der Abstand vom Punkt C zur Ebene E auch durch den Abstand von C zum Punkt F bestimmt werden:
d(C,E) = d(C,F) = \(\left|\begin{pmatrix} 0 \\ 8 \\ 5 \end{pmatrix} - \begin{pmatrix} 1 \\ 4 \\ -2\end{pmatrix}\right| ~=~ \sqrt{1^2+4^2+7^2}~=~\sqrt{66}\approx 8,1\)
Spiegelpunkt C':
Um zum Punkt C' zu gelangen, wird vom Lotfußpunkt F der Vektor \(\vec{CF}\) angelegt:
\(\vec{c'}=\vec{f}+\vec{CF}=\begin{pmatrix} 0 \\ 8 \\ 5 \end{pmatrix}+\begin{pmatrix} -1 \\ 4 \\ 7 \end{pmatrix}=\begin{pmatrix} -1 \\ 12 \\ 12\end{pmatrix}\)
Der Spiegelpunkt C' zu C bzgl. der Ebene E ist C'(-1/12/12).
Anmerkung: Es gilt: \(\vec{c'}=\vec{f}+\vec{CF}= \vec{f}+(\vec{f}-\vec{c})=2\cdot\vec{f}-\vec{c}=2\cdot\begin{pmatrix} 0 \\ 8 \\ 5 \end{pmatrix}-\begin{pmatrix} 1 \\ 4 \\ -2\end{pmatrix}\)\(=\begin{pmatrix} -1 \\ 12 \\ 12\end{pmatrix}\)
zu c)
Die gegenüberliegenden Seiten eines Parallelogramms sind parallel zueinander. Deshalb kann der Punkt D bestimmt werden mit:
\(\vec{d}=\vec{c}+\vec{BA}=\vec{c}+\vec{a}-\vec{b}=\begin{pmatrix} 1 \\ 4 \\ -2 \end{pmatrix}+\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix}-\begin{pmatrix} 8 \\ 6 \\ 4 \end{pmatrix}=\begin{pmatrix} -3 \\ 3 \\ -2 \end{pmatrix}\)
Mit D(-3/3/-2) ist ABCD ein Parallelogramm.
Alternativ: \(\vec{d}=\vec{a}+\vec{BC}=\vec{a}+\vec{c}-\vec{b}\)
zu d)
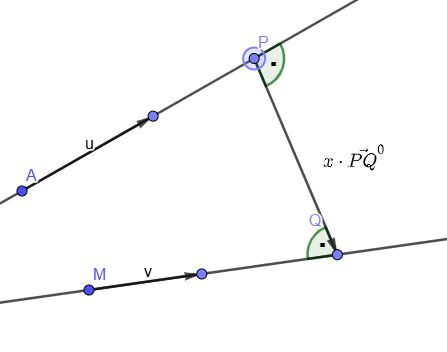
Gerade g: \( \vec{r}~=~\vec{a}+\lambda\vec{u}=\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix} \)
Gerade k: \( \vec{r}~=~\vec{m}+\mu\vec{v}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} ~+~\mu \cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} \)
Seien P und Q die jeweiligen Lotfußpunkte. Der Vektor \(\vec{PQ}\) ist orthogonal zu den Richtungsvektoren der Geraden. Der Abstand x der beiden Geraden entspricht der Länge des Vektors \(\vec{PQ}\):
x = d(g,k) = d(P,Q) = \(\left|\vec{PQ}\right|\) = x ⋅ \(\left|\vec{PQ}^0\right|\).
\(\vec{PQ}^0\) ist der Normaleneinheitsvektor zu \(\vec{PQ}\). Er besitzt die Länge 1 und die Richtung von \(\vec{PQ}\).
Wegen der Orthogonalität zu den Richtungsvektoren ist \(\vec{PQ}^0=(\vec{u}\times\vec{v})^0\) (oder (\(\vec{v}\times\vec{u})^0\)).
Mit \(\vec{PQ}=\vec{u}\times\vec{v}= \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix}\times\begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ -9 \end{pmatrix}\)\(~\rightarrow~(\vec{u}\times\vec{v})^0=\frac{1}{9}\begin{pmatrix} 0 \\ 0 \\ -9 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\)
Es existieren λP und μQ mit:
\( \vec{p}~=~\vec{a}+\lambda_P\cdot\vec{u}=\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} ~+~\lambda_P \cdot \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix} \)
\( \vec{q}~=~\vec{m}+\mu_Q\cdot\vec{v}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} ~+~\mu_Q \cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} \)
Insgesamt gilt:
\(\vec{PQ} = \vec{q}-\vec{p}=x ⋅ \vec{PQ}^0\).
Einsetzen: \(\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} ~+~\mu_Q \cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}-\left(\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} ~+~\lambda_P \cdot \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix}\right)=x\cdot\begin{pmatrix} 0 \\ 0 \\ -1 \end{pmatrix}\)
Neu anordnen:
\(\mu_Q \cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}+\lambda_P \cdot \begin{pmatrix} -4 \\ -1 \\ 0 \end{pmatrix}+x\cdot\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}=\begin{pmatrix} 3 \\ 4 \\ 3 \end{pmatrix}\)
Das sind drei Gleichungen mit drei Unbekannten.
Lösung: μP = \(-\frac{13}{9}\) , λP = \(-\frac{10}{9}\) , x = 3
Anmerkung: Es kann aufgrund der Orientierung der Richtungsvektoren \(\vec{u}\) und \(\vec{v}\) ein negativer Wert für x erscheinen. Für den Abstand der Geraden ist der Betrag von x entscheidend.
μP und λP einsetzen ergibt:
\( \vec{p}~=~\begin{pmatrix} 4 \\ 5 \\ 4 \end{pmatrix} ~-~\frac{10}{9} \cdot \begin{pmatrix} 4 \\ 1 \\ 0 \end{pmatrix}~\rightarrow~P(-\frac{4}{9}/\frac{35}{9}/4) \)
\( \vec{q}~=~\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} ~-~\frac{13}{9}\cdot \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix} ~\rightarrow~Q(-\frac{4}{9}/\frac{35}{9}/1)\)
Die Geraden g und k besitzen den Abstand 3 LE voneinander. Die Lotfußpunkte sind auf der Geraden g der Punkt \(P(-\frac{4}{9}/\frac{35}{9}/4) \) und auf der Geraden k der Punkt \(Q(-\frac{4}{9}/\frac{35}{9}/1)\).
Anmerkung: Die Strecke \(\vec{PQ}\) ist die kürzeste Verbindungsstrecke zwischen den beiden Geraden. Sie besitzt die Länge 3 LE.
a) Bestimmen Sie die Durchstoßpunkte der Kanten der Pyramide durch E.
b) Welchen Winkel bildet die Kante AS mit der Ebene E?
c) Zeichnen Sie die Pyramide und das Trapez in ein KO-System.
d) Bestimmen Sie den Flächeninhalt des Trapezes.
e) Ermitteln Sie den Abstand der Spitze S von der Schnittebene E.
f) Berechnen Sie das Volumen der beiden Teilkörper, in welche die Pyramide durch die Ebene zerlegt wird.
zu a) 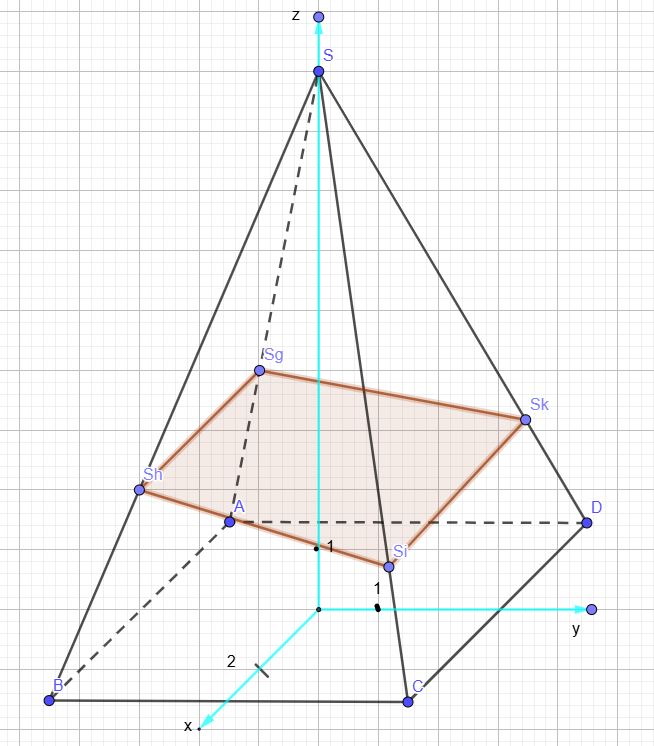
Geraden entlang der Kanten:
(SA) = g: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{a}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix} \)
(SB) = h: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{b}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ -3 \\ -9 \end{pmatrix} \)
(SC) = i: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{c}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ 3 \\ -9 \end{pmatrix} \)
(SD) = k: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{d}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ 3\\ -9 \end{pmatrix} \)
Nun die Schnittpunkte der Geraden mit der Ebene E bestimmen, indem man die Geradengleichung in die Ebenengleichung einsetzt.
g in E einsetzen:
\(\begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}\cdot \left(\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} + \lambda \begin{pmatrix} -3 \\ -3 \\ -9\end{pmatrix}\right)-10=0\) \(~\rightarrow~36-39\cdot\lambda-10=0\) \(~\rightarrow ~\lambda=\frac{26}{39}=\frac{2}{3}\)
Nun λ in g einsetzen:
\( \vec{r}~=~ \begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\frac{2}{3} \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix} ~=~\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix}\)
Der Schnittpunkt von g mit der Ebene E ist Sg(-2/-2/3).
Entsprechend mit den anderen Kanten:
für Gerade h: λ = \(\frac{2}{3}\) → Sh(2/-2/3).
für Gerade i: λ = \(\frac{26}{33}\) → Si(\(\frac{26}{11}\)/\(\frac{26}{11}\)/\(\frac{21}{11}\)).
für Gerade k: λ = \(\frac{26}{33}\) → Sk(\(-\frac{26}{11}\)/\(\frac{26}{11}\)/\(\frac{21}{11}\)).
zu b)
Um den Winkel α zwischen der Ebene E und der Geraden g zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix} \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix}\right|}{\sqrt{17}\cdot\sqrt{99}}~=~arccos\frac{39}{\sqrt{1683}}~\approx~18,1^\circ\)
Der Winkel zwischen der Kante AS und der Grundebene E beträgt α ≈ 71,9°.
Anmerkung: Natürlich kann auch der Normalenvektor \(\begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}\) der Ebene verwendet werden.
Außerdem gilt: cos β = sin α für 0° ≤ α ≤ 90°.
zu c) s. Graphik
zu d)
Flächeninhalt eines Trapezes: AT = \(\frac{1}{2}\)⋅(a + b) ⋅ h, falls a||b.
Hier gilt: a = \(\overline{S_gS_h}\) und b = \(\overline{S_kS_i}\), denn \(\vec{S_gS_h}= \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \) sowie \(\vec{S_kS_i}= \frac{52}{11}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \). Die beiden Vektoren sind kollinear.
Daraus folgt a = 4 und b = \(\frac{52}{11}\).
Die Höhe h des Trapezes ist der Abstand der beiden parallelen Kanten.
Allgemein lässt sich der Abstand zweier paralleler Geraden im R3 bestimmen, indem der Abstand eines Punktes (hier: Sk) auf einer Geraden zur anderen Gerade (hier: durch Sg und Sh) berechnet wird.
Gerade m durch Sg und Sh: \( \vec{r}~=~\vec{s_g}+\lambda\cdot(\vec{s_h}-\vec{s_g})=\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix} \)
Nun wird eine Hilfsebene E' konstruiert, die orthogonal zu m ist und durch den Punkt Sk geht. Der Abstand des Schnittpunktes T der Hilfsebene E' mit der Geraden m und dem Punkt Sk entspricht dem gesuchten Abstand.
E': \(\begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\left(\vec{r}- \frac{1}{11}\begin{pmatrix} -26 \\ 26\\ 21\end{pmatrix}\right) = \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\vec{r}+\frac{104}{11}=0 \)
Nun m in E':
\(\begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\left(\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\right)+\frac{104}{11}=0 \)\(~\rightarrow~-8+4\lambda+\frac{104}{11}=0~\rightarrow~\lambda=-\frac{4}{11}\)
λ in m einsetzen, um T zu ermitteln:
\(\vec{t}=\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~-~\frac{4}{11} \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix} ~\rightarrow~T(-\frac{38}{11}/-2/3)\)
Der Abstand von T zu Sk entspricht der Höhe h des Trapezes:
h = \(\left|\frac{1}{11}\begin{pmatrix} -26 \\ 26 \\ 21 \end{pmatrix}-\frac{1}{11}\begin{pmatrix} -38 \\ -22 \\ 33 \end{pmatrix}\right|\)\(=\left|\frac{1}{11}\begin{pmatrix} 12 \\ 48 \\ -12 \end{pmatrix}\right|~\rightarrow~h=\frac{36}{11}\cdot\sqrt{2}\approx 4,63\)
Daraus folgt die Fläche des Trapezes
AT = \(\frac{1}{2}\left(4+\frac{52}{11}\right)\cdot\frac{36}{11}\cdot\sqrt{2}\approx20,2~FE\)
zu e)
Um den Abstand d eines Punktes von einer Ebene zu bestimmen, wird der Punkt in die Hesseform der Ebenengleichung eingesetzt.
d(S,E) = \( \frac{1}{\sqrt{17}} \left| \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}\cdot\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} -10 \right| = \frac{1}{\sqrt{17}} \left|36-10 \right| \)\( = \frac {26}{\sqrt{17}} \approx6,3\)
Der Abstand des Punktes S von der Ebene E beträgt etwa 6,3 LE.
zu f)
Das Volumen einer Pyramide ist V = \(\frac{1}{3}\cdot G \cdot h\)
Das Volumen der gesamten Pyramide beträgt deshalb: V = \(\frac{1}{3}\cdot6^2\cdot9~=~108~VE\)
Das Volumen des oberen Teilkörpers beträgt Voben = \(\frac{1}{3}\cdot A_T\cdot d(S,E)~\approx~\frac{1}{3}\cdot 20,2\cdot 6,3~\approx~42,4~VE\)
Anmerkung: Die Volumenformel gilt auch für schiefwinklige Pyramiden wegen des Satzes von Cavalieri.
Das Volumen des unteren Teilkörpers beträgt deshalb Vunten ≈ 108 - 42,4 = 65,6 VE.

Geraden entlang der Kanten:
(SA) = g: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{a}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix} \)
(SB) = h: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{b}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ -3 \\ -9 \end{pmatrix} \)
(SC) = i: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{c}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 3 \\ 3 \\ -9 \end{pmatrix} \)
(SD) = k: \( \vec{r}~=~\vec{s}+\lambda\cdot(\vec{d}-\vec{s})=\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ 3\\ -9 \end{pmatrix} \)
Nun die Schnittpunkte der Geraden mit der Ebene E bestimmen, indem man die Geradengleichung in die Ebenengleichung einsetzt.
g in E einsetzen:
\(\begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}\cdot \left(\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} + \lambda \begin{pmatrix} -3 \\ -3 \\ -9\end{pmatrix}\right)-10=0\) \(~\rightarrow~36-39\cdot\lambda-10=0\) \(~\rightarrow ~\lambda=\frac{26}{39}=\frac{2}{3}\)
Nun λ in g einsetzen:
\( \vec{r}~=~ \begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} ~+~\frac{2}{3} \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix} ~=~\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix}\)
Der Schnittpunkt von g mit der Ebene E ist Sg(-2/-2/3).
Entsprechend mit den anderen Kanten:
für Gerade h: λ = \(\frac{2}{3}\) → Sh(2/-2/3).
für Gerade i: λ = \(\frac{26}{33}\) → Si(\(\frac{26}{11}\)/\(\frac{26}{11}\)/\(\frac{21}{11}\)).
für Gerade k: λ = \(\frac{26}{33}\) → Sk(\(-\frac{26}{11}\)/\(\frac{26}{11}\)/\(\frac{21}{11}\)).
zu b)
Um den Winkel α zwischen der Ebene E und der Geraden g zu bestimmen, kann der Winkel β zwischen dem Normalenvektor \(\vec{n}\) der Ebene und dem Richtungsvektor \(\vec{u}\) der Geraden berechnet werden. Es gilt: \(\alpha = 90^\circ - \beta = 90^\circ - \angle(\vec{n},\vec{u})\).
Anmerkung: Der Winkel liegt im Bereich 0 ≤ α ≤ 90°.
Deshalb: \(\beta ~=~arccos\frac{\left|\begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix} \cdot \begin{pmatrix} -3 \\ -3 \\ -9 \end{pmatrix}\right|}{\sqrt{17}\cdot\sqrt{99}}~=~arccos\frac{39}{\sqrt{1683}}~\approx~18,1^\circ\)
Der Winkel zwischen der Kante AS und der Grundebene E beträgt α ≈ 71,9°.
Anmerkung: Natürlich kann auch der Normalenvektor \(\begin{pmatrix} 1 \\ 1 \\ 3 \end{pmatrix}\) der Ebene verwendet werden.
Außerdem gilt: cos β = sin α für 0° ≤ α ≤ 90°.
zu c) s. Graphik
zu d)
Flächeninhalt eines Trapezes: AT = \(\frac{1}{2}\)⋅(a + b) ⋅ h, falls a||b.
Hier gilt: a = \(\overline{S_gS_h}\) und b = \(\overline{S_kS_i}\), denn \(\vec{S_gS_h}= \begin{pmatrix} 4 \\ 0 \\ 0 \end{pmatrix} \) sowie \(\vec{S_kS_i}= \frac{52}{11}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} \). Die beiden Vektoren sind kollinear.
Daraus folgt a = 4 und b = \(\frac{52}{11}\).
Die Höhe h des Trapezes ist der Abstand der beiden parallelen Kanten.
Allgemein lässt sich der Abstand zweier paralleler Geraden im R3 bestimmen, indem der Abstand eines Punktes (hier: Sk) auf einer Geraden zur anderen Gerade (hier: durch Sg und Sh) berechnet wird.
Gerade m durch Sg und Sh: \( \vec{r}~=~\vec{s_g}+\lambda\cdot(\vec{s_h}-\vec{s_g})=\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix} \)
Nun wird eine Hilfsebene E' konstruiert, die orthogonal zu m ist und durch den Punkt Sk geht. Der Abstand des Schnittpunktes T der Hilfsebene E' mit der Geraden m und dem Punkt Sk entspricht dem gesuchten Abstand.
E': \(\begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\left(\vec{r}- \frac{1}{11}\begin{pmatrix} -26 \\ 26\\ 21\end{pmatrix}\right) = \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\vec{r}+\frac{104}{11}=0 \)
Nun m in E':
\(\begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\cdot\left(\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix}\right)+\frac{104}{11}=0 \)\(~\rightarrow~-8+4\lambda+\frac{104}{11}=0~\rightarrow~\lambda=-\frac{4}{11}\)
λ in m einsetzen, um T zu ermitteln:
\(\vec{t}=\begin{pmatrix} -2 \\ -2 \\ 3 \end{pmatrix} ~-~\frac{4}{11} \cdot \begin{pmatrix} 4 \\ 0\\ 0\end{pmatrix} ~\rightarrow~T(-\frac{38}{11}/-2/3)\)
Der Abstand von T zu Sk entspricht der Höhe h des Trapezes:
h = \(\left|\frac{1}{11}\begin{pmatrix} -26 \\ 26 \\ 21 \end{pmatrix}-\frac{1}{11}\begin{pmatrix} -38 \\ -22 \\ 33 \end{pmatrix}\right|\)\(=\left|\frac{1}{11}\begin{pmatrix} 12 \\ 48 \\ -12 \end{pmatrix}\right|~\rightarrow~h=\frac{36}{11}\cdot\sqrt{2}\approx 4,63\)
Daraus folgt die Fläche des Trapezes
AT = \(\frac{1}{2}\left(4+\frac{52}{11}\right)\cdot\frac{36}{11}\cdot\sqrt{2}\approx20,2~FE\)
zu e)
Um den Abstand d eines Punktes von einer Ebene zu bestimmen, wird der Punkt in die Hesseform der Ebenengleichung eingesetzt.
d(S,E) = \( \frac{1}{\sqrt{17}} \left| \begin{pmatrix} 0 \\ 1 \\ 4 \end{pmatrix}\cdot\begin{pmatrix} 0 \\ 0 \\ 9 \end{pmatrix} -10 \right| = \frac{1}{\sqrt{17}} \left|36-10 \right| \)\( = \frac {26}{\sqrt{17}} \approx6,3\)
Der Abstand des Punktes S von der Ebene E beträgt etwa 6,3 LE.
zu f)
Das Volumen einer Pyramide ist V = \(\frac{1}{3}\cdot G \cdot h\)
Das Volumen der gesamten Pyramide beträgt deshalb: V = \(\frac{1}{3}\cdot6^2\cdot9~=~108~VE\)
Das Volumen des oberen Teilkörpers beträgt Voben = \(\frac{1}{3}\cdot A_T\cdot d(S,E)~\approx~\frac{1}{3}\cdot 20,2\cdot 6,3~\approx~42,4~VE\)
Anmerkung: Die Volumenformel gilt auch für schiefwinklige Pyramiden wegen des Satzes von Cavalieri.
Das Volumen des unteren Teilkörpers beträgt deshalb Vunten ≈ 108 - 42,4 = 65,6 VE.
a) Bestimmen Sie die Gleichungen der Geraden g1 und g2, die den Verlauf der Stromschienen beschreiben und zeichnen Sie die Stromschienen in ein Koordinatensystem ein.
b) Die Schülerin L. wendet ein, dass sich die Stromschienen berühren könnten. Zeigen Sie, dass sichergestellt ist, dass die Stromschienen sich nicht berühren.
c) In den Punkten L1( 5 | 3 | 4,5 ) und L2( 2 | 6 | 4,25 ) befinden sich Lampen, die als punktförmige Lichtquellen betrachtet werden können. Weisen Sie nach, dass L1 auf g1 liegt und L2 auf g2, und bestimmen Sie den Abstand der beiden Lampen voneinander. Zeichnen Sie die Lampenpunkte in das Koordinatensystem ein.
d) Der höchste Punkt der Skulptur sei S ( 2 | 4 | 2,25 ). Der Künstler möchte, dass der Schatten dieser Skulpturenspitze noch auf den Fußboden des Raumes (x1-x2-Ebene) und nicht auf eine Wand fällt. Zeigen Sie, dass unter dieser Bedingung nur eine der beiden Lampen eingeschaltet werden darf.
Bestimmen Sie den Schattenpunkt R auf dem Fußboden des Raumes und zeichnen Sie R und S in das Koordinatensystem ein.
e) An die Stromschienen sollen neue Lampen angebracht werden, die von der Schiene 0,2 m vertikal herunterhängen. Beurteilen Sie, ob dies möglich ist, ohne dass dadurch die freie Beweglichkeit der Lampen auf der gesamten oberen Schiene durch die untere Schiene eingeschränkt wird.
Hinweis: Skizzieren Sie die vertikale Projektion der Schienen auf die x1-x2-Ebene, d.h. die x3- Komponente ist Null und betrachten Sie den Höhenunterschied der Schienen über dem Schnittpunkt der Projektionsgeraden.
zu a) 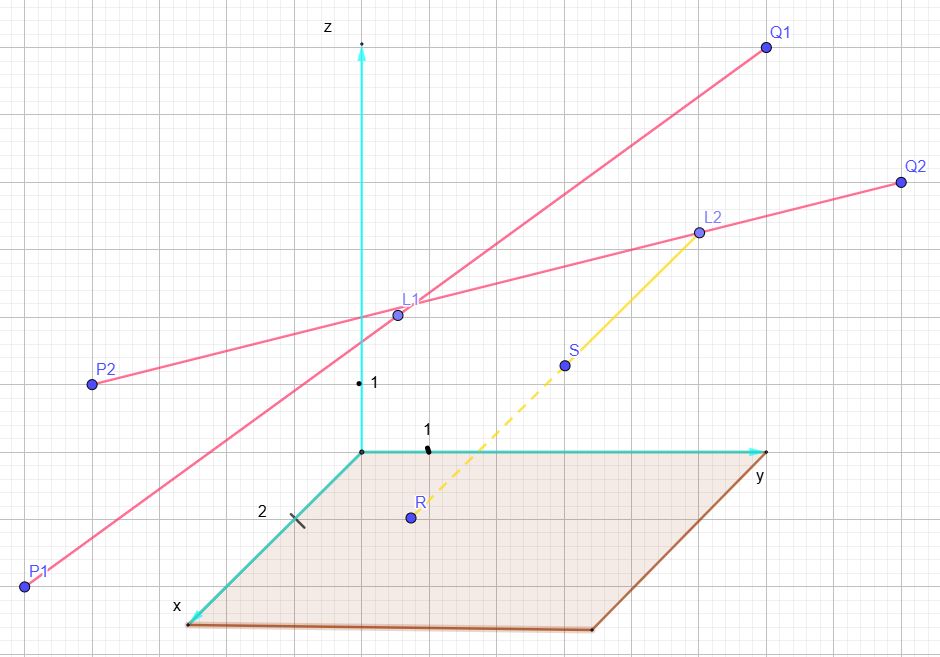
g1: \( \vec{r}~=~\vec{p_1}+\lambda\cdot(\vec{q_1}-\vec{p_1})=\begin{pmatrix} 10 \\ 0 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 3 \end{pmatrix} \)
g2: \( \vec{r}~=~\vec{p_2}+\lambda\cdot(\vec{q_2}-\vec{p_2})=\begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -8 \\ 8 \\ -1 \end{pmatrix} \)
zu b)
Wenn sich die Stromschienen berühren (also einen Schnittpunkt besitzen), müssen die Vektoren \(\vec{P_1Q_1}\), \(\vec{P_2Q_2}\) und \(\vec{P_1P_2}\) komplanar sein. Dies kann am einfachsten mit der Determinante der Vektoren überprüft werden:
det |\(\vec{P_1Q_1}\),\(\vec{P_2Q_2}\),\(\vec{P_1P_2}\)| = \(\begin{vmatrix} -10 &-8&-2\\ 6 &8&0\\ 3 &-1&2\end{vmatrix}=124\neq0\)
Die Vektoren sind nicht komplanar. Die Stromschienen berühren sich nicht.
zu c)
L1 in g1 einsetzen: \( \begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix}~=~\begin{pmatrix} 10 \\ 0 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 3 \end{pmatrix} \)\(~\rightarrow~\lambda=\frac{1}{2}~\rightarrow~L_1\in g_1\)
L2 in g2 einsetzen: \( \begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix}~=~\begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -8 \\ 8 \\ -1 \end{pmatrix} \)\(~\rightarrow~\lambda=\frac{3}{4}~\rightarrow~L_2\in g_2\)
Abstand d(L1,L2) = \(\left|\begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix}-\begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix}\right|\)\(=\left|\begin{pmatrix} -3 \\ 3 \\ -0,25 \end{pmatrix}\right|~=~\sqrt{\frac{289}{16}}~=~ 4,25\)
Die beiden Lampen sind 4,25 m voneinander entfernt.
zu d)
Die Schnittpunkte der Geraden h1 = (L1 , S) und der Geraden h2 = (L2 , S) mit der x1-x2-Grundebene müssen ermittelt werden.
h1: \( \vec{r}~=~\vec{l_1}+\lambda\cdot(\vec{s}-\vec{l_1})=\begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ 1 \\ -2,25 \end{pmatrix} \)
h2: \( \vec{r}~=~\vec{l_2}+\lambda\cdot(\vec{s}-\vec{l_2})=\begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ -2 \\ -2 \end{pmatrix} \)
Bedingung für einen Schnittpunkt mit der x1-x2-Grundebene. x3 = 0.Daraus folgt für
h1: λ = 2 → Schnittpunkt(L1,S) (-1/5/0)
h2: λ = 2,125 → Schnittpunkt(L1,S) (2/1,75/0)
Die x1-Koordinate des Schattenpunktes von L1 auf der x1-x2-Grundebene ist negativ, deshalb darf die Lampe L1 nicht eingeschaltet werden.
Die Lampe L2 wird eingeschaltet. Der Schattenpunkt R der Skulpturenspitze S durch die Lampe L2 ist R( 2/1,75/0).
zu e)
Die Projektionsgeraden der Schienen bzgl. der x1-x2-Grundebene sind:
pg1: \( \vec{r}~=~\begin{pmatrix} 10 \\ 0 \\ 0 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 0 \end{pmatrix} \)
pg2: \( \vec{r}~=~\begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} ~+~\mu \cdot \begin{pmatrix} -8 \\ 8 \\ 0 \end{pmatrix} \)
Durch Gleichsetzen der Geradengleichungen erhält man: λ = \(\frac{1}{2}\) und μ = \(\frac{3}{8}\) und daraus den Schnittpunkt der Projektionsgeraden SP(5/3/0).
Setzt man λ in g1 ein, erhält man für die x3-Koordinate: x3 = 4,5.
Die untere Schiene befindet sich an der Überlappungsstelle bzgl. der x1-x2-Grundebene in 4,5 m Höhe.
Setzt man μ in g2 ein, erhält man für die x3-Koordinate: x3 = 4,625.
Die obere Schiene befindet sich an der Überlappungsstelle bzgl. der x1-x2-Grundebene in 4,625 m Höhe.
Der Höhenunterschied beträgt 0,125 m < 0,2 m. Die neuen Lampen bereiten Probleme.

g1: \( \vec{r}~=~\vec{p_1}+\lambda\cdot(\vec{q_1}-\vec{p_1})=\begin{pmatrix} 10 \\ 0 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 3 \end{pmatrix} \)
g2: \( \vec{r}~=~\vec{p_2}+\lambda\cdot(\vec{q_2}-\vec{p_2})=\begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -8 \\ 8 \\ -1 \end{pmatrix} \)
zu b)
Wenn sich die Stromschienen berühren (also einen Schnittpunkt besitzen), müssen die Vektoren \(\vec{P_1Q_1}\), \(\vec{P_2Q_2}\) und \(\vec{P_1P_2}\) komplanar sein. Dies kann am einfachsten mit der Determinante der Vektoren überprüft werden:
det |\(\vec{P_1Q_1}\),\(\vec{P_2Q_2}\),\(\vec{P_1P_2}\)| = \(\begin{vmatrix} -10 &-8&-2\\ 6 &8&0\\ 3 &-1&2\end{vmatrix}=124\neq0\)
Die Vektoren sind nicht komplanar. Die Stromschienen berühren sich nicht.
zu c)
L1 in g1 einsetzen: \( \begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix}~=~\begin{pmatrix} 10 \\ 0 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 3 \end{pmatrix} \)\(~\rightarrow~\lambda=\frac{1}{2}~\rightarrow~L_1\in g_1\)
L2 in g2 einsetzen: \( \begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix}~=~\begin{pmatrix} 8 \\ 0 \\ 5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -8 \\ 8 \\ -1 \end{pmatrix} \)\(~\rightarrow~\lambda=\frac{3}{4}~\rightarrow~L_2\in g_2\)
Abstand d(L1,L2) = \(\left|\begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix}-\begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix}\right|\)\(=\left|\begin{pmatrix} -3 \\ 3 \\ -0,25 \end{pmatrix}\right|~=~\sqrt{\frac{289}{16}}~=~ 4,25\)
Die beiden Lampen sind 4,25 m voneinander entfernt.
zu d)
Die Schnittpunkte der Geraden h1 = (L1 , S) und der Geraden h2 = (L2 , S) mit der x1-x2-Grundebene müssen ermittelt werden.
h1: \( \vec{r}~=~\vec{l_1}+\lambda\cdot(\vec{s}-\vec{l_1})=\begin{pmatrix} 5 \\ 3 \\ 4,5 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -3 \\ 1 \\ -2,25 \end{pmatrix} \)
h2: \( \vec{r}~=~\vec{l_2}+\lambda\cdot(\vec{s}-\vec{l_2})=\begin{pmatrix} 2 \\ 6 \\ 4,25 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 0 \\ -2 \\ -2 \end{pmatrix} \)
Bedingung für einen Schnittpunkt mit der x1-x2-Grundebene. x3 = 0.Daraus folgt für
h1: λ = 2 → Schnittpunkt(L1,S) (-1/5/0)
h2: λ = 2,125 → Schnittpunkt(L1,S) (2/1,75/0)
Die x1-Koordinate des Schattenpunktes von L1 auf der x1-x2-Grundebene ist negativ, deshalb darf die Lampe L1 nicht eingeschaltet werden.
Die Lampe L2 wird eingeschaltet. Der Schattenpunkt R der Skulpturenspitze S durch die Lampe L2 ist R( 2/1,75/0).
zu e)
Die Projektionsgeraden der Schienen bzgl. der x1-x2-Grundebene sind:
pg1: \( \vec{r}~=~\begin{pmatrix} 10 \\ 0 \\ 0 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} -10 \\ 6 \\ 0 \end{pmatrix} \)
pg2: \( \vec{r}~=~\begin{pmatrix} 8 \\ 0 \\ 0 \end{pmatrix} ~+~\mu \cdot \begin{pmatrix} -8 \\ 8 \\ 0 \end{pmatrix} \)
Durch Gleichsetzen der Geradengleichungen erhält man: λ = \(\frac{1}{2}\) und μ = \(\frac{3}{8}\) und daraus den Schnittpunkt der Projektionsgeraden SP(5/3/0).
Setzt man λ in g1 ein, erhält man für die x3-Koordinate: x3 = 4,5.
Die untere Schiene befindet sich an der Überlappungsstelle bzgl. der x1-x2-Grundebene in 4,5 m Höhe.
Setzt man μ in g2 ein, erhält man für die x3-Koordinate: x3 = 4,625.
Die obere Schiene befindet sich an der Überlappungsstelle bzgl. der x1-x2-Grundebene in 4,625 m Höhe.
Der Höhenunterschied beträgt 0,125 m < 0,2 m. Die neuen Lampen bereiten Probleme.
 Das Koordinatensystem sei weiterhin so gewählt, dass die vier Eckpunkte des Towers auf dem Boden die folgenden Koordinaten haben (Längeneinheit: 1 m):
Das Koordinatensystem sei weiterhin so gewählt, dass die vier Eckpunkte des Towers auf dem Boden die folgenden Koordinaten haben (Längeneinheit: 1 m):