b) Gegeben ist die Funktion f(x) = \(\sqrt{1+x}\).
Begründen Sie durch eine Taylorreihenentwicklung von f an der Stelle x0 die Näherungsformel \(\sqrt{1+x}\approx 1+\frac{1}{2}x\) für 0 < x << 1.
zu a)
Taylorreihenentwicklung von f an der Stelle x0: $$f(x)=\sum_{n=0}^{\infty}\frac{1}{n!}\cdot f^{(n)}(x_0)\cdot (x-x_0)^n$$
Entwickelt man f(x) = cos x an der Stelle x0 = 0, erhält man: $$cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...$$
zu b)
f an der Stelle x0 als Tayloreihe darstellen und nach dem 1. Glied abbrechen:
Es gilt f '(x) = \(\frac{1}{2\sqrt{1+x}}\), also f '(0) = \(\frac{1}{2\sqrt{1+0}} = \frac{1}{2}\). Deshalb
$$f(x)=\sqrt{1+x}\approx \frac{1}{0!}f^{(0)}(0)x^0+\frac{1}{1!}f^{(1)}(0)x^1=1\cdot 1\cdot 1+1 \cdot \frac{1}{2}\cdot x$$
Falls 0 < x << 1 (also sehr klein ist), kann die Reihenentwicklung nach dem ersten Glied abgebrochen werden, weil die Summanden mit den höheren Potenzen von x dann vernachlässigbar klein werden.
Man sieht: für -1 << x < 0 gilt dann \(\sqrt{1+x}\approx 1-\frac{1}{2}x\).
Taylorreihenentwicklung von f an der Stelle x0: $$f(x)=\sum_{n=0}^{\infty}\frac{1}{n!}\cdot f^{(n)}(x_0)\cdot (x-x_0)^n$$
Entwickelt man f(x) = cos x an der Stelle x0 = 0, erhält man: $$cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\frac{1}{6!}x^6+...$$
zu b)
f an der Stelle x0 als Tayloreihe darstellen und nach dem 1. Glied abbrechen:
Es gilt f '(x) = \(\frac{1}{2\sqrt{1+x}}\), also f '(0) = \(\frac{1}{2\sqrt{1+0}} = \frac{1}{2}\). Deshalb
$$f(x)=\sqrt{1+x}\approx \frac{1}{0!}f^{(0)}(0)x^0+\frac{1}{1!}f^{(1)}(0)x^1=1\cdot 1\cdot 1+1 \cdot \frac{1}{2}\cdot x$$
Falls 0 < x << 1 (also sehr klein ist), kann die Reihenentwicklung nach dem ersten Glied abgebrochen werden, weil die Summanden mit den höheren Potenzen von x dann vernachlässigbar klein werden.
Man sieht: für -1 << x < 0 gilt dann \(\sqrt{1+x}\approx 1-\frac{1}{2}x\).
b) Bestimmen Sie für die Funktion f(x) = x3 die Stelle stärkster Krümmung und den zugehörigen Krümmungsradius.
zu a) 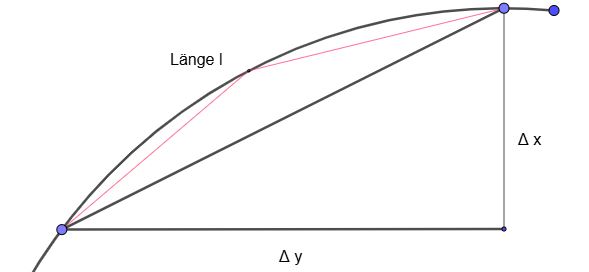
Analog zur Bestimmung der Fläche unterhalb eines Graphen kann auch die Länge eines Graphen im Intervall [a,b] ermittelt werden. In diesem Fall wird der Bogen durch die Länge der Sekante angenähert. Durch Grenzwertbildung gelangt man zum Ergebnis.
Länge der Sekante im Intervall [a,b]: \(l=(\sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2 }\cdot \Delta x\)
Das Intervall [a,b] wird nun in n Teilintervalle zerlegt und die Länge des Bogens l als Summe der Teilintervalle geschrieben. Lässt man die Anzahl der Teilintervalle gegen unendlich gehen und schreibt Δ als d, gelangt man zur Integraldarstellung \(l=\int_{a}^{b} \sqrt{1+(f '(x))^2}dx\) (*).
Angewendet auf die gegebene Funktion f im Intervall [2;3] mit f '(x) = \(\sqrt{x}\):
\(l=\int_{2}^{3} \sqrt{1+(f '(x))^2}~dx~=~\int_{2}^{3} \sqrt{1+x}~dx~=~\frac{2}{3}\cdot(1+x)^{\frac{3}{2}}~|_{2}^{3}\)\(~=~\frac{2}{3}\cdot(4^{\frac{3}{2}}-3^{\frac{3}{2}})\approx1,87\)
zu b)
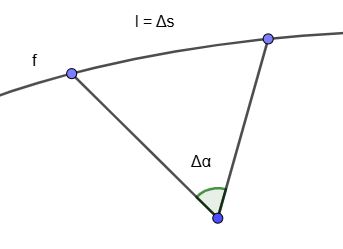
Die Krümmung K ist definiert als das Verhältnis von Winkeländerung Δ α zu Bogenlänge l = Δ s: K = \(lim \frac{\Delta\alpha}{\Delta s}\).
Der Krümmungsradius R entspricht dem Kehrwert der Krümmung K: R = \(\frac{1}{K}\)
Je stärker die Krümmung ist, desto kleiner ist der Krümmungsradius.
Es gilt: K(x) = \(\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}\)
Sonderfälle sind Wendepunkte, denn dort gilt f ''(x) = 0.
Herleitung:
K(x) = \(\frac{\Delta\alpha}{\Delta s}=\frac{\Delta\alpha}{\Delta x}\frac{\Delta x}{\Delta s}\).
Für den Faktor \(\frac{\Delta x}{\Delta s}\) gilt \(\frac{\Delta x}{\Delta s} = \frac{1}{\sqrt{1+(f '(x))^2}}\), denn dieser Faktor ist einfach der Kehrwert der Ableitung der Bogenlänge l =Δ s - einfach das Argument des Integrals verwenden s. oben(*).
Für den Faktor \(\frac{\Delta\alpha}{\Delta s}\) bemüht man die Ableitung des arctan und die Kettenregel.
Allgemein: f '(x) = tan α und deshalb α = arctan f '(x).
Deshalb: \(\frac{\Delta\alpha}{\Delta x}~=~\frac{f ''(x)}{1+(f '(x))^2}\)
Alles einsetzen: K(x) = \(\frac{\Delta\alpha}{\Delta x}\frac{\Delta x}{\Delta s}~=~\frac{f ''(x)}{1+(f '(x))^2} \cdot \frac{1}{\sqrt{1+(f '(x))^2}}~=~\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}\)
Nun wird f bzw. f ' und f '' in die Gleichung für die Krümmung eingesetzt:
K(x) = \(\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}~=~\frac{6x}{(1+9x^4)^{\frac{3}{2}}}\)
Um die Stelle stärkster Krümmung zu ermitteln, benötigt man die erste Ableitung von K:
K'(x) = \(\frac{6\cdot(1+9x^4)^{\frac{3}{2}}-36x^3\cdot 1,5\cdot(1+9x^4)^{\frac{1}{2}}\cdot 6x}{(1+9x^4)^3}~=~\frac{6\cdot(1+9x^4)-324x^4}{(1+9x^4)^{\frac{5}{2}}}\)\(~=~\frac{6-270x^4}{(1+9x^4)^{\frac{5}{2}}}\)
Notwendige Bedingung für ein Extremum ist K'(xE) = 0.
Ein Bruch wird nur Null, wenn der Zähler Null wird.
Deshalb: 6 - 270x4 = 0 → xE1,2 = ±\(\frac{1}{\sqrt[4]{45}}\approx \pm0,386\)
An den Stellen ±0,386 ist die Krümmung des Graphen von f(x) = x3 am stärksten. Sie beträgt dort K(±0,386) ≈ ±1,76.
Der Krümmungsradius ist R = \(\frac{1}{K}\approx0,567\).

Analog zur Bestimmung der Fläche unterhalb eines Graphen kann auch die Länge eines Graphen im Intervall [a,b] ermittelt werden. In diesem Fall wird der Bogen durch die Länge der Sekante angenähert. Durch Grenzwertbildung gelangt man zum Ergebnis.
Länge der Sekante im Intervall [a,b]: \(l=(\sqrt{(\Delta x)^2 + (\Delta y)^2} = \sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2 }\cdot \Delta x\)
Das Intervall [a,b] wird nun in n Teilintervalle zerlegt und die Länge des Bogens l als Summe der Teilintervalle geschrieben. Lässt man die Anzahl der Teilintervalle gegen unendlich gehen und schreibt Δ als d, gelangt man zur Integraldarstellung \(l=\int_{a}^{b} \sqrt{1+(f '(x))^2}dx\) (*).
Angewendet auf die gegebene Funktion f im Intervall [2;3] mit f '(x) = \(\sqrt{x}\):
\(l=\int_{2}^{3} \sqrt{1+(f '(x))^2}~dx~=~\int_{2}^{3} \sqrt{1+x}~dx~=~\frac{2}{3}\cdot(1+x)^{\frac{3}{2}}~|_{2}^{3}\)\(~=~\frac{2}{3}\cdot(4^{\frac{3}{2}}-3^{\frac{3}{2}})\approx1,87\)
zu b)

Die Krümmung K ist definiert als das Verhältnis von Winkeländerung Δ α zu Bogenlänge l = Δ s: K = \(lim \frac{\Delta\alpha}{\Delta s}\).
Der Krümmungsradius R entspricht dem Kehrwert der Krümmung K: R = \(\frac{1}{K}\)
Je stärker die Krümmung ist, desto kleiner ist der Krümmungsradius.
Es gilt: K(x) = \(\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}\)
Sonderfälle sind Wendepunkte, denn dort gilt f ''(x) = 0.
Herleitung:
K(x) = \(\frac{\Delta\alpha}{\Delta s}=\frac{\Delta\alpha}{\Delta x}\frac{\Delta x}{\Delta s}\).
Für den Faktor \(\frac{\Delta x}{\Delta s}\) gilt \(\frac{\Delta x}{\Delta s} = \frac{1}{\sqrt{1+(f '(x))^2}}\), denn dieser Faktor ist einfach der Kehrwert der Ableitung der Bogenlänge l =Δ s - einfach das Argument des Integrals verwenden s. oben(*).
Für den Faktor \(\frac{\Delta\alpha}{\Delta s}\) bemüht man die Ableitung des arctan und die Kettenregel.
Allgemein: f '(x) = tan α und deshalb α = arctan f '(x).
Deshalb: \(\frac{\Delta\alpha}{\Delta x}~=~\frac{f ''(x)}{1+(f '(x))^2}\)
Alles einsetzen: K(x) = \(\frac{\Delta\alpha}{\Delta x}\frac{\Delta x}{\Delta s}~=~\frac{f ''(x)}{1+(f '(x))^2} \cdot \frac{1}{\sqrt{1+(f '(x))^2}}~=~\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}\)
Nun wird f bzw. f ' und f '' in die Gleichung für die Krümmung eingesetzt:
K(x) = \(\frac{f ''(x)}{(1+(f '(x))^2)^{\frac{3}{2}}}~=~\frac{6x}{(1+9x^4)^{\frac{3}{2}}}\)
Um die Stelle stärkster Krümmung zu ermitteln, benötigt man die erste Ableitung von K:
K'(x) = \(\frac{6\cdot(1+9x^4)^{\frac{3}{2}}-36x^3\cdot 1,5\cdot(1+9x^4)^{\frac{1}{2}}\cdot 6x}{(1+9x^4)^3}~=~\frac{6\cdot(1+9x^4)-324x^4}{(1+9x^4)^{\frac{5}{2}}}\)\(~=~\frac{6-270x^4}{(1+9x^4)^{\frac{5}{2}}}\)
Notwendige Bedingung für ein Extremum ist K'(xE) = 0.
Ein Bruch wird nur Null, wenn der Zähler Null wird.
Deshalb: 6 - 270x4 = 0 → xE1,2 = ±\(\frac{1}{\sqrt[4]{45}}\approx \pm0,386\)
An den Stellen ±0,386 ist die Krümmung des Graphen von f(x) = x3 am stärksten. Sie beträgt dort K(±0,386) ≈ ±1,76.
Der Krümmungsradius ist R = \(\frac{1}{K}\approx0,567\).
a) Untersuchen Sie f auf Nullstellen. Bestimmen Sie das Symmetrieverhalten von Gf und zeigen Sie, dass die Geraden mit den Gleichungen y = −1 und y = 1 Asymptoten von Gf sind.
b) Zeigen Sie, dass f streng monoton zunehmend ist. Berechnen Sie f(1) sowie f '(0) und skizzieren Sie Gf unter Verwendung aller bisherigen Ergebnisse in ein Koordinatensystem.
c) Berechnen Sie den Term einer Stammfunktion von f.
( mögliches Ergebnis: F(x) = ln(ex+e-x) + C )
d) f besitzt eine Umkehrfunktion f -1. Geben Sie die Definitionsmenge von f -1 an und bestimmen Sie für f -1 einen Funktionsterm.
( mögliches Ergebnis: f -1(x) = \(\frac{1}{2}ln\frac{1+x}{1-x}\) )
Hinweis: Erweitern Sie den Term von f mit ex.
e) Die Fallgeschwindigkeit eines Fallschirmspringers vor Öffnen des Schirms wird in guter Näherung beschrieben durch den Term v(t) = 50⋅f(0,2t) = \(50\cdot\frac{e^{0,2t}-e^{-0,2t}}{e^{0,2t}+e^{-0,2t}}\) mit t ≥ 0.
Dabei ist t die Maßzahl der Fallzeit in Sekunden, v(t) die Maßzahl der Fallgeschwindigkeit in \(\frac{m}{s}\).
i) Berechnen Sie \(\lim_{t \to \infty} v(t)\) und deuten Sie das Ergebnis im genannten Anwendungsbezug.
ii) Berechnen Sie auf eine Dezimale gerundet die Zeit, nach der der Springer
eine Geschwindigkeit von \(49\frac{m}{s}\) erreicht hat.
Die Absprunghöhe wird als genügend groß vorausgesetzt.
iii) Die Maßzahl der in der Zeit 11,5 s durchfallenen Strecke (in m) ist gegeben durch \(\int_{0}^{11,5} v(t)~ dt\).
Berechnen Sie dieses Integral.
f) Gegeben ist eine auf R definierte Funktion h, deren Funktionsgleichung in der Form y = h(x) = \(\frac{g(x)}{g~'(x)}\) geschrieben werden kann. g ist hierbei eine Funktion, die mit ihrer zweiten Ableitung übereinstimmt, d. h. es gilt g''(x) = g(x) für alle x ∈ R . Die Funktion f ist ein Beispiel für eine derartige Funktion h.
i) Zeigen Sie, dass für alle x∈R gilt: h'(x) = 1 − [h(x)]2.
ii) Folgern Sie aus der Gleichung von Teilaufgabe fi: Verläuft der Graph von h
im Streifen −1 < y < 1, dann steigt er dort streng monoton.
zu a)
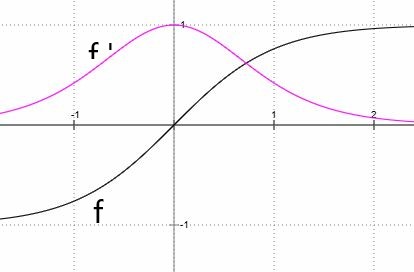
Bedingung für Nullstellen: f(xN) = 0 → \(\large{\frac{e^{x_N}-e^{-x_N}}{e^{x_N}+e^{-x_N}}}~=~0\)
Zähler Null setzen: \(\large{e^{x_N}-e^{-x_N}}~=~0~~\rightarrow~~\large{e^{x_N}}~=~\large{e^{-x_N}}\)
Logarithmieren: xN = -xN → xN = 0 → N(0/0)
Der Graph von f ist punktsymmetrisch. Dann muss man zeigen: -f(x) = f(-x).
f(-x) = \(\frac{e^{-x}-e^{x}}{e^{-x}+e^{x}}~=~-\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~-f(x)\)
Um die Asymptoten zu ermitteln, betrachtet man x → ±∞.
\(\lim_{x \to \infty}\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\lim_{x \to \infty}\frac{e^x}{e^x}~=~1\), denn e-x → 0 für x → ∞.
\(\lim_{x \to {-\infty}}\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\lim_{x \to {-\infty}}\frac{-e^{-x}}{e^{-x}}~=~-1\), denn ex → 0 für x → -∞
zu b)
streng monoton zunehmend: \(\forall x_1
Es ist empfehlenswert, aus der Behauptung etwas Wahres äquivalent abzuleiten. Formal wird dann der Beweis der Behauptung umgekehrt aufgeschrieben (also aus etwas Wahrem die Behauptung abgeleitet).
Es sei x1 < x2:
\(\frac{e^{x_1}-e^{-x_1}}{e^{x_1}+e^{-x_1}}<\frac{e^{x_2}-e^{-x_2}}{e^{x_2}+e^{-x_2}}\)\(~\iff~(e^{x_1}-e^{-x_1})\cdot(e^{x_2}+e^{-x_2})~<~(e^{x_2}-e^{-x_2})\cdot(e^{x_1}+e^{-x_1})\)
\(~\iff~e^{x_1}e^{x_2}+e^{x_1}e^{-x_2}-e^{-x_1}e^{x_2}-e^{-x_1}e^{-x_2}~<~e^{x_1}e^{x_2}+e^{-x_1}e^{x_2}-e^{x_1}e^{-x_2}-e^{-x_1}e^{-x_2}\)
Vereinfachen durch Termumformung:
\(~\iff~e^{x_1}e^{-x_2}-e^{-x_1}e^{x_2}~<~e^{-x_1}e^{x_2}-e^{x_1}e^{-x_2}\)
Term weiter umformen:
\(~\iff~2\cdot e^{x_1}e^{-x_2}~<~2\cdot e^{-x_1}e^{x_2}~\iff~e^{x_1}e^{-x_2}~<~e^{-x_1}e^{x_2}\)
Term weiter umformen:
\(~\iff 1~<~e^{2\cdot(x_2-x_1)}\)
Nach Voraussetzung ist x1 < x2, der Exponent somit positiv. Der Wert der Exponentialfunktion zur Basis e mit diesem Exponenten ist deshalb größer als 1.
Die Behauptung, dass f streng monoton ist, ist somit wahr. Wie gesagt: formal den Beweis umgekehrt aufschreiben. Das ist möglich, weil nur Äquivalenzumformungen durchgeführt wurden.
f(1) = \(\frac{e^1-e^{-1}}{e^1+e^{-1}}~\approx~0,76\)
f '(x) = \(\frac{(e^x-e^{-x})\cdot (e^{-x}-e^{x})}{(e^x+e^{-x})^2}~+~1\) → f '(1) = \(\frac{(e^1-e^{-1})\cdot (e^{-1}-e^{1})}{(e^1+e^{-1})^2}~+~1\approx 0,42\)
zu c)
Man erkennt, beim Funktionsterm entspricht der Zähler der Ableitung des Nenners.
Für die Funktion H(x) = ln x ist die Ableitung h(x) =\(\frac{1}{x}\).
Die Substitutionsregel lautet: \(\int g'(x)h(g(x))dx~=~H(g(x)) + C\).
Sei nun g(x) = \(e^x+e^{-x}\).
Dann ist \(\int (e^x-e^{-x})\frac{1}{e^x+e^{-x}}dx~=~\int g'(x)h(g(x))dx~=~H(g(x)) + C~=~ln(e^x+e^{-x})+C\).
zu d)
Der Definitionsbereich der Umkehrfunktion entspricht dem Wertebereich der Funktion: \(D_{f^{-1}}=W_f\).
Da f streng monoton ist und die Asymptoten y = ±1 sind, ist das (offene) Intervall ]-1;1[ der Definitionsbereich von f-1.
Bestimmung der Umkehrfunktion f -1:
f(x) = y = \(\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\frac{e^{2x}-1}{e^{2x}+1}\) (Erweiterung mit ex)
nach x auflösen:
y⋅(e2x + 1) = e2x - 1 ↔ 1 + y =(1 - y)⋅e2x ↔ \(e^{2x}=\frac{1+y}{1-y}\)
Logarithmieren: \(2x~=~ln\frac{1+y}{1-y} ~\iff~x~=~f^{-1}(y)~=~\frac{1}{2}ln\frac{1+y}{1-y}\)
zu e)
i.
\(\lim_{t \to \infty}(50\cdot\frac{e^{0,2t}-e^{-0,2t}}{e^{0,2t}+e^{-0,2t}})~=~\lim_{t \to \infty}(50\cdot\frac{e^{0,4t}-1}{e^{0,4t}+1})~=~50\cdot1~=~50\)
Der Wert 50 \(\frac{m}{s}\) entspricht der Grenzgeschwindigkeit des Fallschirmspringers. Aufgrund seines Luftwiderstands wächst die Reibungskraft mit zunehmender Geschwindigkeit an. Die Gravitationskraft bleibt jedoch (annähernd) gleich. Bei Erreichen der Grenzgeschwindigkeit sind Reibung und Gravitation (entgegengesetzt) gleich.
ii.
Ansatz: \(50\cdot\frac{e^{0,2t}-e^{-0,2t}}{e^{0,2t}+e^{-0,2t}}~=~49~~\iff~~50\cdot\frac{e^{0,4t}-1}{e^{0,4t}+1}~=~49\)
\(\iff~~\frac{e^{0,4t}-1}{e^{0,4t}+1}~=~0,98~~\iff~~e^{0,4t}-1~=~0,98\cdot (e^{0,4t}+1) \)
\(\iff~~0,02\cdot e^{0,4t}~=~1,98 ~~\iff~~0,4t~=~ln\frac{1,98}{0,02}~~\iff~~t~\approx~11,5~s\)
Nach etwa 11,5 Sekunden erreicht der Springer eine Geschwindigkeit von 49 \(\frac{m}{s}\).
iii.
\(\int_{0}^{11,5} v(t)~ dt~=~ln(e^x+e^{-x}|_{0}^{11,5}~=~ln(e^{11,5}+e^{-11,5}-(e^0+e^{-0}))~=~98,7\).
Nach fast 100 m erreicht der Springer eine Geschwindigkeit von 49 \(\frac{m}{s}\).
zu f)
i.
Sei h(x) = \(\frac{g(x)}{g '(x)}\) mit g(x) = g''(x) abgekürzt g = g''.
Dann h'(x) = \(\frac{g ~'\cdot g~'-g\cdot g~''}{g~'~^2}~=~\frac{g~'\cdot g~'-g\cdot g}{g~'~^2}~=~\frac{g~'~^2-g^2}{g~'~^2}~=~1-\frac{g^2}{g~'~^2}~=~1-h^2\)
ii.
Wenn der Graph von h im Streifen −1 < y < 1 verläuft, gilt: |h(x)| < 1.
Außerdem soll gelten: h'(x) = 1 − [h(x)]2. Insgesamt folgt daraus: h'(x) > 0.
Die Steigung des Graphen von h ist für jedes x positiv (0 < h'(x) < 1). Dann ist h streng monoton steigend.

Bedingung für Nullstellen: f(xN) = 0 → \(\large{\frac{e^{x_N}-e^{-x_N}}{e^{x_N}+e^{-x_N}}}~=~0\)
Zähler Null setzen: \(\large{e^{x_N}-e^{-x_N}}~=~0~~\rightarrow~~\large{e^{x_N}}~=~\large{e^{-x_N}}\)
Logarithmieren: xN = -xN → xN = 0 → N(0/0)
Der Graph von f ist punktsymmetrisch. Dann muss man zeigen: -f(x) = f(-x).
f(-x) = \(\frac{e^{-x}-e^{x}}{e^{-x}+e^{x}}~=~-\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~-f(x)\)
Um die Asymptoten zu ermitteln, betrachtet man x → ±∞.
\(\lim_{x \to \infty}\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\lim_{x \to \infty}\frac{e^x}{e^x}~=~1\), denn e-x → 0 für x → ∞.
\(\lim_{x \to {-\infty}}\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\lim_{x \to {-\infty}}\frac{-e^{-x}}{e^{-x}}~=~-1\), denn ex → 0 für x → -∞
zu b)
streng monoton zunehmend: \(\forall x_1
Es sei x1 < x2:
\(\frac{e^{x_1}-e^{-x_1}}{e^{x_1}+e^{-x_1}}<\frac{e^{x_2}-e^{-x_2}}{e^{x_2}+e^{-x_2}}\)\(~\iff~(e^{x_1}-e^{-x_1})\cdot(e^{x_2}+e^{-x_2})~<~(e^{x_2}-e^{-x_2})\cdot(e^{x_1}+e^{-x_1})\)
\(~\iff~e^{x_1}e^{x_2}+e^{x_1}e^{-x_2}-e^{-x_1}e^{x_2}-e^{-x_1}e^{-x_2}~<~e^{x_1}e^{x_2}+e^{-x_1}e^{x_2}-e^{x_1}e^{-x_2}-e^{-x_1}e^{-x_2}\)
Vereinfachen durch Termumformung:
\(~\iff~e^{x_1}e^{-x_2}-e^{-x_1}e^{x_2}~<~e^{-x_1}e^{x_2}-e^{x_1}e^{-x_2}\)
Term weiter umformen:
\(~\iff~2\cdot e^{x_1}e^{-x_2}~<~2\cdot e^{-x_1}e^{x_2}~\iff~e^{x_1}e^{-x_2}~<~e^{-x_1}e^{x_2}\)
Term weiter umformen:
\(~\iff 1~<~e^{2\cdot(x_2-x_1)}\)
Nach Voraussetzung ist x1 < x2, der Exponent somit positiv. Der Wert der Exponentialfunktion zur Basis e mit diesem Exponenten ist deshalb größer als 1.
Die Behauptung, dass f streng monoton ist, ist somit wahr. Wie gesagt: formal den Beweis umgekehrt aufschreiben. Das ist möglich, weil nur Äquivalenzumformungen durchgeführt wurden.
f(1) = \(\frac{e^1-e^{-1}}{e^1+e^{-1}}~\approx~0,76\)
f '(x) = \(\frac{(e^x-e^{-x})\cdot (e^{-x}-e^{x})}{(e^x+e^{-x})^2}~+~1\) → f '(1) = \(\frac{(e^1-e^{-1})\cdot (e^{-1}-e^{1})}{(e^1+e^{-1})^2}~+~1\approx 0,42\)
zu c)
Man erkennt, beim Funktionsterm entspricht der Zähler der Ableitung des Nenners.
Für die Funktion H(x) = ln x ist die Ableitung h(x) =\(\frac{1}{x}\).
Die Substitutionsregel lautet: \(\int g'(x)h(g(x))dx~=~H(g(x)) + C\).
Sei nun g(x) = \(e^x+e^{-x}\).
Dann ist \(\int (e^x-e^{-x})\frac{1}{e^x+e^{-x}}dx~=~\int g'(x)h(g(x))dx~=~H(g(x)) + C~=~ln(e^x+e^{-x})+C\).
zu d)
Der Definitionsbereich der Umkehrfunktion entspricht dem Wertebereich der Funktion: \(D_{f^{-1}}=W_f\).
Da f streng monoton ist und die Asymptoten y = ±1 sind, ist das (offene) Intervall ]-1;1[ der Definitionsbereich von f-1.
Bestimmung der Umkehrfunktion f -1:
f(x) = y = \(\frac{e^x-e^{-x}}{e^x+e^{-x}}~=~\frac{e^{2x}-1}{e^{2x}+1}\) (Erweiterung mit ex)
nach x auflösen:
y⋅(e2x + 1) = e2x - 1 ↔ 1 + y =(1 - y)⋅e2x ↔ \(e^{2x}=\frac{1+y}{1-y}\)
Logarithmieren: \(2x~=~ln\frac{1+y}{1-y} ~\iff~x~=~f^{-1}(y)~=~\frac{1}{2}ln\frac{1+y}{1-y}\)
zu e)
i.
\(\lim_{t \to \infty}(50\cdot\frac{e^{0,2t}-e^{-0,2t}}{e^{0,2t}+e^{-0,2t}})~=~\lim_{t \to \infty}(50\cdot\frac{e^{0,4t}-1}{e^{0,4t}+1})~=~50\cdot1~=~50\)
Der Wert 50 \(\frac{m}{s}\) entspricht der Grenzgeschwindigkeit des Fallschirmspringers. Aufgrund seines Luftwiderstands wächst die Reibungskraft mit zunehmender Geschwindigkeit an. Die Gravitationskraft bleibt jedoch (annähernd) gleich. Bei Erreichen der Grenzgeschwindigkeit sind Reibung und Gravitation (entgegengesetzt) gleich.
ii.
Ansatz: \(50\cdot\frac{e^{0,2t}-e^{-0,2t}}{e^{0,2t}+e^{-0,2t}}~=~49~~\iff~~50\cdot\frac{e^{0,4t}-1}{e^{0,4t}+1}~=~49\)
\(\iff~~\frac{e^{0,4t}-1}{e^{0,4t}+1}~=~0,98~~\iff~~e^{0,4t}-1~=~0,98\cdot (e^{0,4t}+1) \)
\(\iff~~0,02\cdot e^{0,4t}~=~1,98 ~~\iff~~0,4t~=~ln\frac{1,98}{0,02}~~\iff~~t~\approx~11,5~s\)
Nach etwa 11,5 Sekunden erreicht der Springer eine Geschwindigkeit von 49 \(\frac{m}{s}\).
iii.
\(\int_{0}^{11,5} v(t)~ dt~=~ln(e^x+e^{-x}|_{0}^{11,5}~=~ln(e^{11,5}+e^{-11,5}-(e^0+e^{-0}))~=~98,7\).
Nach fast 100 m erreicht der Springer eine Geschwindigkeit von 49 \(\frac{m}{s}\).
zu f)
i.
Sei h(x) = \(\frac{g(x)}{g '(x)}\) mit g(x) = g''(x) abgekürzt g = g''.
Dann h'(x) = \(\frac{g ~'\cdot g~'-g\cdot g~''}{g~'~^2}~=~\frac{g~'\cdot g~'-g\cdot g}{g~'~^2}~=~\frac{g~'~^2-g^2}{g~'~^2}~=~1-\frac{g^2}{g~'~^2}~=~1-h^2\)
ii.
Wenn der Graph von h im Streifen −1 < y < 1 verläuft, gilt: |h(x)| < 1.
Außerdem soll gelten: h'(x) = 1 − [h(x)]2. Insgesamt folgt daraus: h'(x) > 0.
Die Steigung des Graphen von h ist für jedes x positiv (0 < h'(x) < 1). Dann ist h streng monoton steigend.