b) Berechnen Sie die folgenden Determinanten:
zu a)
Definition 'Vektor': Ein Vektor ist die Menge aller gleich langen, gleich gerichteten und gleich orientierten Pfeile.
Anmerkung 1: Zeichnet man konkret einen Pfeil, bezeichnet man ihn üblicherweise als Vektor, obwohl er nur ein Repräsentant eines Vektors ist (denn ein Vektor ist eine Menge von Pfeilen).
Anmerkung 2: Etwas abstraktere Definition: Als Vektor bezeichnet man ein Element eines Vektorraums.
Definition 'lineare Unabhängigkeit von Vektoren': (mit ai ∈ R)
$$\vec{x_0},~ \vec{x_1},~...,~\vec{x_n}~ lin~ unabhängig~~\leftrightarrow~~(a_0\cdot\vec{x_0}+a_1\cdot\vec{x_1}+...+a_n\cdot\vec{x_n}=\vec{0}~\rightarrow~\forall i~a_i=0 ~einzige~ Lösung)$$ zu b)
= 2 ⋅ (-2) - 3 ⋅ 3 = -13 = -37
Definition 'Vektor': Ein Vektor ist die Menge aller gleich langen, gleich gerichteten und gleich orientierten Pfeile.
Anmerkung 1: Zeichnet man konkret einen Pfeil, bezeichnet man ihn üblicherweise als Vektor, obwohl er nur ein Repräsentant eines Vektors ist (denn ein Vektor ist eine Menge von Pfeilen).
Anmerkung 2: Etwas abstraktere Definition: Als Vektor bezeichnet man ein Element eines Vektorraums.
Definition 'lineare Unabhängigkeit von Vektoren': (mit ai ∈ R)
$$\vec{x_0},~ \vec{x_1},~...,~\vec{x_n}~ lin~ unabhängig~~\leftrightarrow~~(a_0\cdot\vec{x_0}+a_1\cdot\vec{x_1}+...+a_n\cdot\vec{x_n}=\vec{0}~\rightarrow~\forall i~a_i=0 ~einzige~ Lösung)$$ zu b)
= 2 ⋅ (-2) - 3 ⋅ 3 = -13 = -37
a) Überprüfen Sie, ob einer der Vektoren kollinear zum Vektor ist.
b) Zeigen Sie, dass die Vektoren eine Basis des R3 bilden und berechnen Sie für die Koordinaten bzgl dieser Basis.
zu a)
Zwei Vektoren sind kollinear (also linear abhängig), wenn ein Vektor ein Vielfaches des anderen ist.
Es muss demnach eine reelle Zahl k geben mit .
Aus folgt: → → → es existiert ein k.
Folgerung: sind kollinear.
Aus folgt: → → → es existiert kein k.
Folgerung: sind nicht kollinear.
Aus folgt: → → → es existiert kein k.
Folgerung: sind nicht kollinear.
zu b)
Am einfachsten ist es, die Determinante, die durch die Vektoren gegeben ist, zu überprüfen:
det () ≠ 0 ↔ linear unabhängig
det () = = 3 → linear unabhängig
→ Die Vektoren bilden eine Basis des R3.
Dann kann der Vektor als Linearkombination der Vektoren dargestellt werden:
→ (lin. Gleichungssystem)
→
Zwei Vektoren sind kollinear (also linear abhängig), wenn ein Vektor ein Vielfaches des anderen ist.
Es muss demnach eine reelle Zahl k geben mit .
Aus folgt: → → → es existiert ein k.
Folgerung: sind kollinear.
Aus folgt: → → → es existiert kein k.
Folgerung: sind nicht kollinear.
Aus folgt: → → → es existiert kein k.
Folgerung: sind nicht kollinear.
zu b)
Am einfachsten ist es, die Determinante, die durch die Vektoren gegeben ist, zu überprüfen:
det () ≠ 0 ↔ linear unabhängig
det () = = 3 → linear unabhängig
→ Die Vektoren bilden eine Basis des R3.
Dann kann der Vektor als Linearkombination der Vektoren dargestellt werden:
→ (lin. Gleichungssystem)
→
a) Geben Sie die Gerade g durch die Punkte A und B an.
b) Bestimmen Sie einen weiteren Punkt auf der Geraden g und zeigen Sie, dass C nicht auf der Geraden liegt.
c) Wie lautet die Gerade g’, die parallel zu g ist und durch C verläuft?
d) Ermitteln Sie den Punkt D (4/y/z), der auf der Geraden g liegt.
zu a)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu b)
weiterer Punkt E: z.B. λ = -1 setzen.
Dann: \( \vec{e}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~(-1) \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} ~=~ \begin{pmatrix} 1 \\ 1 \\ 6 \end{pmatrix}~~\rightarrow~~E(1/1/6) \)
zu c)
Parallele Geraden besitzen kollineare Richtungsvektoren.
g': \( \vec{r}~=~ \begin{pmatrix} 1 \\ -1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu d)
Ortsvektor \( \vec{d}\) in g einsetzen und λ bestimmen. Daraus die fehlenden Koordinaten berechnen.
Also: \( \begin{pmatrix} 4 \\ y \\ z \end{pmatrix}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix}~~\rightarrow~~\lambda~=~2~(wegen~4=2+\lambda\cdot1)~~\rightarrow~~D(4/1/-3) \)
Mit der 2-Punkte -Form folgt: g: \( \vec{r}~=~ \vec{a}~+~\lambda\cdot(\vec{b}-\vec{a})~~\rightarrow~~\vec{r}~=~\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu b)
weiterer Punkt E: z.B. λ = -1 setzen.
Dann: \( \vec{e}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~(-1) \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} ~=~ \begin{pmatrix} 1 \\ 1 \\ 6 \end{pmatrix}~~\rightarrow~~E(1/1/6) \)
zu c)
Parallele Geraden besitzen kollineare Richtungsvektoren.
g': \( \vec{r}~=~ \begin{pmatrix} 1 \\ -1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix} \)
zu d)
Ortsvektor \( \vec{d}\) in g einsetzen und λ bestimmen. Daraus die fehlenden Koordinaten berechnen.
Also: \( \begin{pmatrix} 4 \\ y \\ z \end{pmatrix}~=~ \begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix} ~+~\lambda \cdot \begin{pmatrix} 1 \\ 0 \\ -3 \end{pmatrix}~~\rightarrow~~\lambda~=~2~(wegen~4=2+\lambda\cdot1)~~\rightarrow~~D(4/1/-3) \)
a) Zeichnen Sie das Vierflach.
b) Drücken Sie die Vektoren als Linarkombination der Vektoren aus.
c) Geben Sie die Koordinaten von N und M an.
d) Untersuchen Sie, ob sich die Gerade g durch N und M sowie die Gerade h durch S und B schneiden.
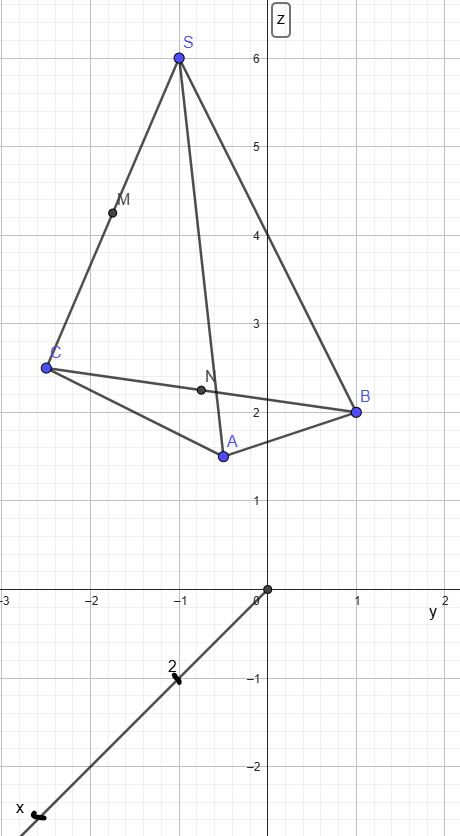 zu a)
zu a)s.Bild
zu b)
Vektorzüge durchführen:
\( \vec{BS}~=~\vec{BA}~+~\vec{AS}~=~-\vec{a}~+~\vec{c}\)
\( \vec{AM}=\vec{AC}+\vec{CM}=\vec{b}+\frac{1}{2}\vec{CS}=\vec{b}+\frac{1}{2}(\vec{CA}+\vec{AS})=\vec{b}+\frac{1}{2}(-\vec{b}+\vec{c})=\frac{1}{2}\vec{b}+\frac{1}{2}\vec{c}\)
\( \vec{NM}=\vec{NC}+\vec{CM}=\frac{1}{2}\vec{BC}+\vec{CM}=\frac{1}{2}(\vec{BA}+\vec{AC})+\frac{1}{2}(\vec{CA}+\vec{AS})=\frac{1}{2}(-\vec{a}+\vec{b})+\frac{1}{2}(-\vec{b}+\vec{c})=-\frac{1}{2}\vec{a}+\frac{1}{2}\vec{b}+\frac{1}{2}\vec{c}\)
zu c)
M ist der Mittelpunkt der Strecke CS: \( \vec{m}=\frac{1}{2} (\begin{pmatrix} 7 \\ 1 \\ 6 \end{pmatrix} +\begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix})= \begin{pmatrix} 5,5 \\ 1 \\ 7 \end{pmatrix} ~~\rightarrow~~M(5,5/1/7) \)
N ist der Mittelpunkt der Strecke BC: \( \vec{n}=\frac{1}{2} (\begin{pmatrix} 6 \\ 4 \\ 5 \end{pmatrix} +\begin{pmatrix} 7 \\ 1 \\ 6 \end{pmatrix})= \begin{pmatrix} 6,5 \\ 2,5 \\ 5,5 \end{pmatrix} ~~\rightarrow~~N(6,5/2,5/5,5) \)
zu d)
Gerade g: \( \vec{r}~=~\begin{pmatrix} 6,5 \\ 2,5 \\ 5,5 \end{pmatrix} ~+~\lambda^{'}~\begin{pmatrix} -1 \\ -1,5 \\ 1,5 \end{pmatrix}~=~\begin{pmatrix} 6,5 \\ 2,5 \\ 5,5 \end{pmatrix} ~+~\lambda~\begin{pmatrix} 2 \\ 3 \\ -3 \end{pmatrix} \)
Gerade h: \( \vec{r}~=~\begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} ~+~\mu~\begin{pmatrix} 2 \\ 3 \\ -3 \end{pmatrix} \)
Da die Richtungsvektoren der Geraden g und h identisch (und damit kollinear) sind, sind beide Geraden parallel zueinander.
Nun muss man noch prüfen, ob beide Geraden identisch sind. Dazu genügt es, einen Ortsvektor in die andere Geradengleichung einzusetzen:
\( \begin{pmatrix} 6,5 \\ 2,5 \\ 5,5 \end{pmatrix}~=~\begin{pmatrix} 4 \\ 1 \\ 8 \end{pmatrix} ~+~\mu~\begin{pmatrix} 2 \\ 3 \\ -3 \end{pmatrix} ~\rightarrow~ \begin{array}{c} 6,5=4+2\mu \\ 2,5=1+2\mu \\ 5,5=8-3\mu \end{array}~\rightarrow~ \begin{array}{c} \mu=1,25 \\ \mu=0,75 \\ \mu=5/6 \end{array}\)
Da es kein gemeinsames μ gibt, sind die Geraden echt parallel.
Natürlich kann man auch einfacher argumentieren:
Die Geraden durch CS und CB als Strahlen bilden zusammen mit den Geraden g und h eine Strahlensatzfigur mit dem Zentrum C. Da M und N jeweils die Mittelpunkte der Strecken CS und CB darstellen, sind die Geraden g und h parallel. Die Strecke NM ist deshalb halb so lang wie die Strecke BS. Die Geraden g und h schneiden sich deshalb nicht.
a) Geben Sie die Transformationsmatrix an, die kartesische Koordinaten in die Koordinaten der Basis B umrechnet.
b) Geben Sie die kartesischen Koordinaten der Punkte P(3/4) sowie Q(2/-1) in Koordinaten der Basis B an.
zu a)
Um die Transformationsmatrix MK->B zu erhalten, müssen die Basisvektoren der kartesischen Basis durch die Basisvektoren der Basis B ausgedrückt werden.
\( \begin{pmatrix} 1 \\ 0 \end{pmatrix}~=~\lambda \begin{pmatrix} 1 \\ 1 \end{pmatrix} ~+~\mu~\begin{pmatrix} -3 \\ 2 \end{pmatrix} ~\rightarrow~ \begin{array}{c} 1=\lambda-3\mu \\ 0=\lambda+2\mu \end{array}~\rightarrow~ \lambda=\frac{2}{5}~,~ \mu=-\frac{1}{5} \)
sowie
\( \begin{pmatrix} 0 \\ 1 \end{pmatrix}~=~\lambda \begin{pmatrix} 1 \\ 1 \end{pmatrix} ~+~\mu~\begin{pmatrix} -3 \\ 2 \end{pmatrix} ~\rightarrow~ \begin{array}{c} 0=\lambda-3\mu \\ 1=\lambda+2\mu \end{array}~\rightarrow~ \lambda=\frac{3}{5}~,~ \mu=\frac{1}{5} \)
Daraus ergibt sich die Transformationsmatrix MK->B = \( \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \)
zu b)
Nun kann man kartesische Koordinaten in Koordinaten bzgl der Basis B umrechnen:
\( \vec{p}_{B} = M_{K \rightarrow B} \cdot \vec{p}_{K} \)
Für P: \( \vec{p}_{B} = \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \begin{pmatrix} \frac{18}{5} \\ \frac{1}{5} \end{pmatrix}\)
Für Q: \( \vec{q}_{B} = \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \cdot \begin{pmatrix} 2 \\ -1 \end{pmatrix} = \begin{pmatrix} \frac{1}{5} \\ -\frac{3}{5} \end{pmatrix}\)
Anmerkung: Die Transformationsmatrix MB->K = \( \begin{pmatrix} 1 & -3 \\ 1 & 2 \end{pmatrix} \) ist sofort darzustellen.
Eine Transformationsmatrix ist die Inverse der anderen.
Um die Transformationsmatrix MK->B zu erhalten, müssen die Basisvektoren der kartesischen Basis durch die Basisvektoren der Basis B ausgedrückt werden.
\( \begin{pmatrix} 1 \\ 0 \end{pmatrix}~=~\lambda \begin{pmatrix} 1 \\ 1 \end{pmatrix} ~+~\mu~\begin{pmatrix} -3 \\ 2 \end{pmatrix} ~\rightarrow~ \begin{array}{c} 1=\lambda-3\mu \\ 0=\lambda+2\mu \end{array}~\rightarrow~ \lambda=\frac{2}{5}~,~ \mu=-\frac{1}{5} \)
sowie
\( \begin{pmatrix} 0 \\ 1 \end{pmatrix}~=~\lambda \begin{pmatrix} 1 \\ 1 \end{pmatrix} ~+~\mu~\begin{pmatrix} -3 \\ 2 \end{pmatrix} ~\rightarrow~ \begin{array}{c} 0=\lambda-3\mu \\ 1=\lambda+2\mu \end{array}~\rightarrow~ \lambda=\frac{3}{5}~,~ \mu=\frac{1}{5} \)
Daraus ergibt sich die Transformationsmatrix MK->B = \( \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \)
zu b)
Nun kann man kartesische Koordinaten in Koordinaten bzgl der Basis B umrechnen:
\( \vec{p}_{B} = M_{K \rightarrow B} \cdot \vec{p}_{K} \)
Für P: \( \vec{p}_{B} = \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \cdot \begin{pmatrix} 3 \\ 4 \end{pmatrix} = \begin{pmatrix} \frac{18}{5} \\ \frac{1}{5} \end{pmatrix}\)
Für Q: \( \vec{q}_{B} = \begin{pmatrix} \frac{2}{5} & \frac{3}{5} \\ -\frac{1}{5} & \frac{1}{5} \end{pmatrix} \cdot \begin{pmatrix} 2 \\ -1 \end{pmatrix} = \begin{pmatrix} \frac{1}{5} \\ -\frac{3}{5} \end{pmatrix}\)
Anmerkung: Die Transformationsmatrix MB->K = \( \begin{pmatrix} 1 & -3 \\ 1 & 2 \end{pmatrix} \) ist sofort darzustellen.
Eine Transformationsmatrix ist die Inverse der anderen.
| VIA | BODYMED | BRAINDRAIN | |
|---|---|---|---|
| Kohlehydrate | 30 | 20 | 25 |
| Eiweiß | 20 | 45 | 55 |
| Fette | 50 | 35 | 20 |
Er möchte einen Trunk mixen, der 25% Kohlehydrate, 45% Eiweiß und 30% Fette enthält. Welche Anteile an den drei Mitteln sind dafür erforderlich? Zeigen Sie, dass man damit keinen Drink mixen kann, der 30% Kohlehydrate, 40% Eiweiß und 30% Fette mixen kann.
Seien x, y und z die jeweiligen (positiven) Anteile der Produkte VIA, BODYMED und BRAINDRAIN.Dann gilt:
\( \begin{array}{c} Kohlehydrate:~~ \\ Eiweiß: \\ Fette: \end{array}\begin{array}{c} 30x+20y+25z=25 \\ 20x+45y+55z=45 \\ 50x+35y+20z=30 \end{array}~\rightarrow~ x=\frac{2}{9}~,~~y=\frac{2}{9}~,~~z=\frac{5}{9}\)
Das Mixgetränk besteht aus jeweils gut 22% Anteile von VIA und BODYMED sowie knapp 56% Anteil von BRAINDRAIN.
Für einen Drink, der 30% Kohlehydrate, 40% Eiweiß und 30% Fette enthält, müsste man wegen der Kohlenhydrate schon zu 100% VIA verwenden. Dann stimmen aber die Anteile an Eiweiß und Fetten nicht.
Man kann es aber auch rechnerisch nachweisen:
\( \begin{array}{c} Kohlehydrate:~~ \\ Eiweiß: \\ Fette: \end{array}\begin{array}{c} 30x+20y+25z=30 \\ 20x+45y+55z=40 \\ 50x+35y+20z=30 \end{array}~\rightarrow~ x=\frac{5}{9}~,~~y=\frac{-4}{9}~,~~z=\frac{8}{9}\)
Die rechnerische Lösung erfordert einen negativen Anteil an BODYMED. Das ist im Sachzusammenhang natürlich sinnfrei.
\( \begin{array}{c} Kohlehydrate:~~ \\ Eiweiß: \\ Fette: \end{array}\begin{array}{c} 30x+20y+25z=25 \\ 20x+45y+55z=45 \\ 50x+35y+20z=30 \end{array}~\rightarrow~ x=\frac{2}{9}~,~~y=\frac{2}{9}~,~~z=\frac{5}{9}\)
Das Mixgetränk besteht aus jeweils gut 22% Anteile von VIA und BODYMED sowie knapp 56% Anteil von BRAINDRAIN.
Für einen Drink, der 30% Kohlehydrate, 40% Eiweiß und 30% Fette enthält, müsste man wegen der Kohlenhydrate schon zu 100% VIA verwenden. Dann stimmen aber die Anteile an Eiweiß und Fetten nicht.
Man kann es aber auch rechnerisch nachweisen:
\( \begin{array}{c} Kohlehydrate:~~ \\ Eiweiß: \\ Fette: \end{array}\begin{array}{c} 30x+20y+25z=30 \\ 20x+45y+55z=40 \\ 50x+35y+20z=30 \end{array}~\rightarrow~ x=\frac{5}{9}~,~~y=\frac{-4}{9}~,~~z=\frac{8}{9}\)
Die rechnerische Lösung erfordert einen negativen Anteil an BODYMED. Das ist im Sachzusammenhang natürlich sinnfrei.
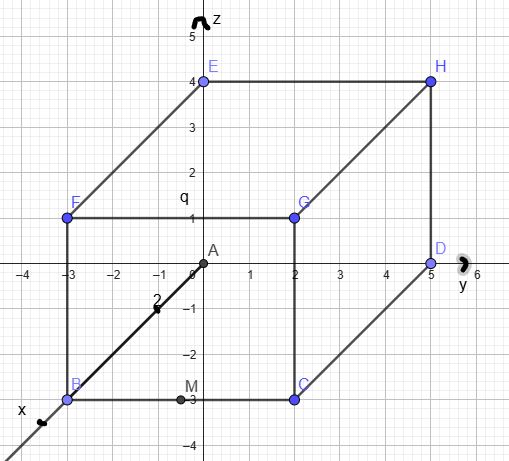 zu a)
zu a)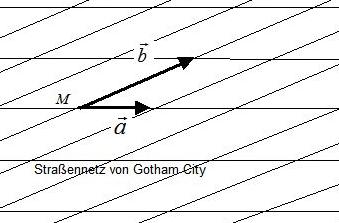 Die Basis B von Gotham City besteht aus den Basisvektoren und .
Die Basis B von Gotham City besteht aus den Basisvektoren und .