Gruppen

In diesem Abschnitt geht es darum, grundlegende Eigenschaften für ein ‚vernünftiges‘ Rechnen zu beschreiben. Diese grundlegenden Eigenschaften werden Axiome genannt. Die Idee ist, aus diesen allgemein formulierten Bedingungen weitere Folgerungen abzuleiten, die dann für jedes Gebilde gelten, die den Axiomen genügen! In einem konkreten Fall genügt es also, nur die Gültigkeit der Axiome nachzuweisen und dann können alle Folgerungen auf den konkreten Fall angewendet werden.

Als kleine Motivationshilfe für das nur scheinbar abstrakte Thema mag die Information dienen, dass der britische Mathematiker Alan Touring während des 2. Weltkrieges mit Hilfe der Gruppentheorie den deutschen Geheimcode 'knackte' und so maßgeblich zur Verkürzung des Krieges beitrug und dadurch zahllose Menschenleben bewahrte.

Kommen wir zur Definition der sogenannten Gruppenaxiome!

Ein Paar ( M , ᵒ ) bestehend aus einer Menge M und einer Verknüpfung ᵒ heißt Gruppe, wenn folgende Axiome erfüllt sind:

1. Abgeschlossenheit:

Für alle Elemente a und b aus der Menge M gilt, dass die Verknüpfung a ᵒ b wieder eine Element der Menge ist:

$$ (\forall a, b \in M) \text{ }a \text{ }ᵒ \text{ }b \in M $$

Dies garantiert, dass man beim Rechnen die gegebene Menge M nicht ‚verlässt‘.

2. Assoziativgesetz:

$$ (\forall a, b, c \in M) \text{ }(a \text{ }ᵒ \text{ }b) \text{ }ᵒ \text{ }c \text{ }= \text{ } a \text{ }ᵒ \text{ }(b \text{ }ᵒ \text{ }c) $$

Dieses Axiom garantiert, dass es bei der Verknüpfung mehrerer Elemente egal ist, in welcher Reihenfolge die Verknüpfung vorgenommen wird. Achtung: Die Reihenfolge der Elemente bleibt aber erhalten!

3. Existenz eines neutrales Elements:

In der Menge M existiert ein Element n, dass bei einer Verknüpfung mit einem anderen Element a nichts bewirkt:

$$ (\exists n \in M) (\forall a \in M) \text{ }a \text{ }ᵒ \text{ }n \text{ }= \text{ } n \text{ }ᵒ \text{ } a $$

Das neutrale Element wird häufig 0 (Null) genannt. Man kann beweisen, dass es genau ein neutrales Element in einer Gruppe gibt und dass es egal ist, ob man es von rechts oder von links mit einem Element verknüpft.

4. Existenz von inversen Elementen:

Zu jedem Element a der Menge gibt es ein sogenanntes inverses Element a^-1, sodass die Verknüpfung beider Elemente das neutrale Element n ergibt.

$$ (\forall a \in M) (\exists a^{-1} \in M) \text{ } a \text{ }ᵒ \text{ }a^{-1} \text{ }= \text{ } n $$

Die Schreibweise a^-1 hat keine rechentechnische Bedeutung. Es ist nur eine Kennzeichnung für das inverse Element von a.
Man achte auf die Reihenfolge des All- und des Existenzquantors. Sie ist nicht vertauschbar. Beispiel: Zu jedem Topf (also für alle Töpfe) gibt es einen passenden Deckel, aber es existiert kein Deckel, der auf alle Töpfe passt!
Auch hier lässt sich beweisen, dass es zu jedem Element genau ein inverses Element in der Gruppe gibt und dass es egal ist, ob man von links oder rechts mit dem inversen Element verknüpft.

5. Kommutativgesetz:

Gilt das Kommutativ- oder Vertauschungsgesetz, spricht man von einer abelschen oder kommutativen Gruppe.

$$ (\forall a, b \in M) \text{ }a \text{ }ᵒ \text{ }b \text{ } =\text{ }b \text{ }ᵒ \text{ }a $$

Beispiele

(ℕ , +)	Menge der natürlichen Zahlen mit der Verknüpfung +	keine Gruppe, denn es gilt zwar die Abgeschlossenheit, auch das Assoziativgesetz ist gültig und es gibt ein neutrales Element - die 0 - , aber es gibt nicht unbedingt inverse Elemente. Denn das inverse Element zu 2 ist -2. -2 ist aber keine natürliche Zahl.
(ℤ , +)	Menge der ganzen Zahlen mit der Verknüpfung +	abelsche Gruppe, denn nun sind auch die inversen Elemente in der Menge enthalten: z.B. zu 2 ist es -2 usw.
(ℤ\{0} , ·)	Menge der ganzen Zahlen ohne die Null mit der Verknüpfung ·	keine Gruppe, denn es gilt zwar die Abgeschlossenheit, auch das Assoziativgesetz ist gültig und es gibt ein neutrales Element - die 1 - , aber es gibt nicht unbedingt inverse Elemente. Denn das inverse Element zu 2 ist 1/2. 1/2 ist aber keine ganze Zahl.
(ℚ , +)	Menge der rationalen Zahlen mit der Verknüpfung +	abelsche Gruppe, denn es gilt zwar die Abgeschlossenheit, auch das Assoziativgesetz ist gültig und es gibt ein neutrales Element - die 1 - , aber es gibt nicht unbedingt inverse Elemente. Denn das inverse Element zu 2 ist 1/2. 1/2 ist aber keine ganze Zahl.
(ℚ\{0} , ·)	Menge der rationalen Zahlen ohne die Null mit der Verknüpfung ·	abelsche Gruppe, nun sind die inversen Elemente in derMenge enthalten.
(ℝ , +)	Menge der reellen Zahlen mit der Verknüpfung +	abelsche Gruppe
(ℝ\{0} , ·)	Menge der reellen Zahlen ohne die Null mit der Verknüpfung ·	abelsche Gruppe

Man erkennt, dass die Zahlbereichserweiterungen, die im Laufe der Schulzeit durchgeführt wurden, wesentlich der Einführung inverser Elemente geschuldet sind, um 'vernünftig' rechnen zu können.

Die in den bisherigen Beispielen genannten Zahlmengen haben unendlich viele Elemente. In den folgeneden Beispielen betrachten wir endliche Mengen.

Da das 3. Axiom die Existenz eines neutralen Elements fordert, muss eine Gruppe mindestens 1 Element enthalten.

Am einfachsten gelingt die Darstellung der Verknüfung in endlichen Mengen mit einer sogenannten 'Verknüpfungstafel'. Es können nicht nur sämtliche Verknüpfungen abgelesen werden, sondern man erkennt auch das neutrale Element sowie die jeweiligen inversen Elemente. Die Gültigkeit des Kommutativgesetzes ist ebenfalls ablesbar.

Verknüpfungstafel 1 Element M = { 0 }:

+	0
0	0

Einzig mögliche Verknüpfung: 0 + 0 = 0

Verknüpfungstafel 2 Elemente M = { 0 , 1 }:

+	0	1
0	0	1
1	1	0

mögliche Verknüpfungen: 0 + 0 = 0 0 + 1 = 1

1 + 0 = 1 1 + 1 = 0

Eine andere Möglichkeit für die Verknüpfung von 1 mit sich selbst als 0 gibt es nicht. 2 kommt nicht in Frage, weil dann die Abgeschlossenheit der Verknüpfung nicht mehr erfüllt ist, 1 geht auch nicht, weil es ansonsten kein inverses Element zu 1 gäbe. Sowohl 0 als auch 1 sind zu sich selbst invers. Diese Eigenschaft eines Elements heißt involutorisch.

Korrekt müsste es also heißen: 1 und 1 ist 2, wenn nicht 0. Letzteres in der Gruppe mit 2 Elementen.

Verknüpfungstafel 3 Elemente M = { 0 , 1 , 2 }:

+	0	1	2
0	0	1	2
1	1	2	0
2	2	0	1

0 ist das neutrale Element. Man erkennt das neutrale Element daran, dass seine Spalte mit der Spalte ganz links identisch sein muss.

In jeder Spalte muss auch das neutrale Element vorkommen, weil man daran das inverse Element erkennen kann: beispielsweise ist das zu 2 inverse Element hier 1.

Nachvollziehen lassen sich diese ungewöhnlichen Verknüpfungen am besten, wenn man die Restklassen- oder Modulo-Rechnung zugrunde legt. Bei einer Modulo-Rechnung betrachtet man nur den Rest einer ganzzahligen Division. So ist 7 mod 3 = 1, denn 7 : 3 = 2 Rest 1.

Rest 2 und Rest 1 addieren sich zu 3. Das ist bei einer Modulo-Rechnung aber wieder 0, denn 3 mod 3 = 0.

Modulo-Rechnungen spielen beispielsweise bei kryptographischen Vefahren eine wichtige Rolle.

In der Verknüpfungstafel dürfen nur Elemente der Menge auftauchen. Deshalb gilt die Abgeschlossenheit. Das Vorhandensein eines neutralen Elements sowie der inversen Elemente wurde schon erläutert. Das Kommutativgesetz ist gültig, wenn man die Werte in der Tafel an der Hauptdiagonalen (von links oben nach recht unten) spiegeln kann. Fehlt noch die Gültigkeit des Assoziativgesetzes. Dies lässt sich nur überprüfen, wenn man alle Möglichkeiten (bei endlichen Gruppen) berechnet. Das sind im Fall der Gruppe mit 3 Elementen 3³ = 27 Gleichungen, die überprüft werden müssen. Hier sollte man zumindest Stichproben machen.

Beispiel Gruppe mit 3 Elementen: (2 + 1) + 2 = 0 + 2 = 2 = 2 + 0 = 2 + (1 + 2) usw.

Aufgaben: Erstelle Verknüpfungstafeln für Gruppen mit 4 bzw. 5 Elementen.

+	0	1	2	3
0	0	1	2	3
1	1	2	3	0
2	2	3	0	1
3	3	0	1	2

+	0	1	2	3	4
0	0	1	2	3	4
1	1	2	3	4	0
2	2	3	4	0	1
3	3	4	0	1	2
4	4	0	1	2	3

Die bisherigen Beispielen benennen nur Zahlmengen. Nun betrachten wir Mengen, deren Elemente Abbildungen sind. Die Verknüpfung ist die Hintereinanderausführung (HEA) zweier Abbildungen.

Beispiel:

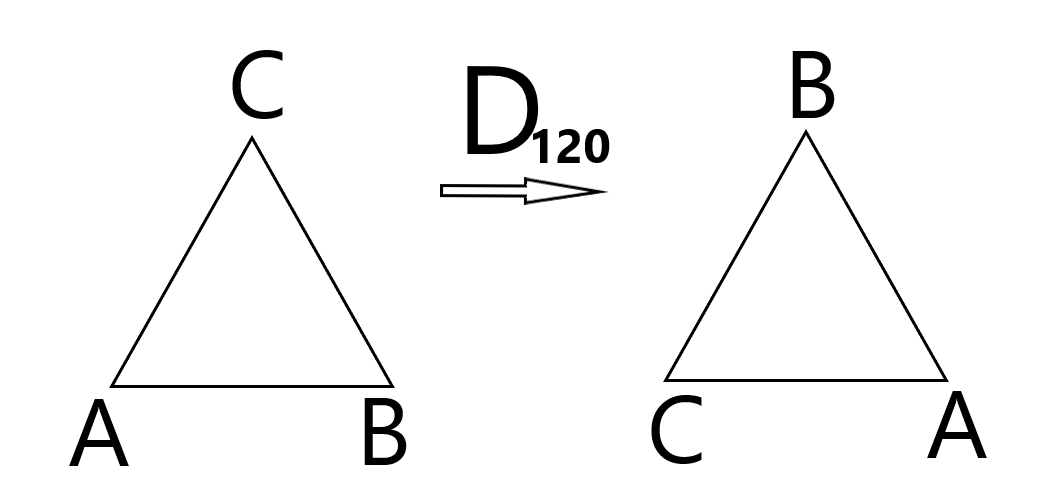
Ein gleichseitiges Dreieck soll um den Mittelpunkt mathematisch positiv (also entgegen dem Uhrzeigersinn) gedreht werden. Erlaubte Drehwinkel sind 0^o, 120^o sowie 240^o. Durch eine derartige Drehung werden Eckpunkte des Dreiecks wieder auf seine Eckpunkte abgebildet. Eine Drehung um 360^o entspricht einer Drehung um 0^o.

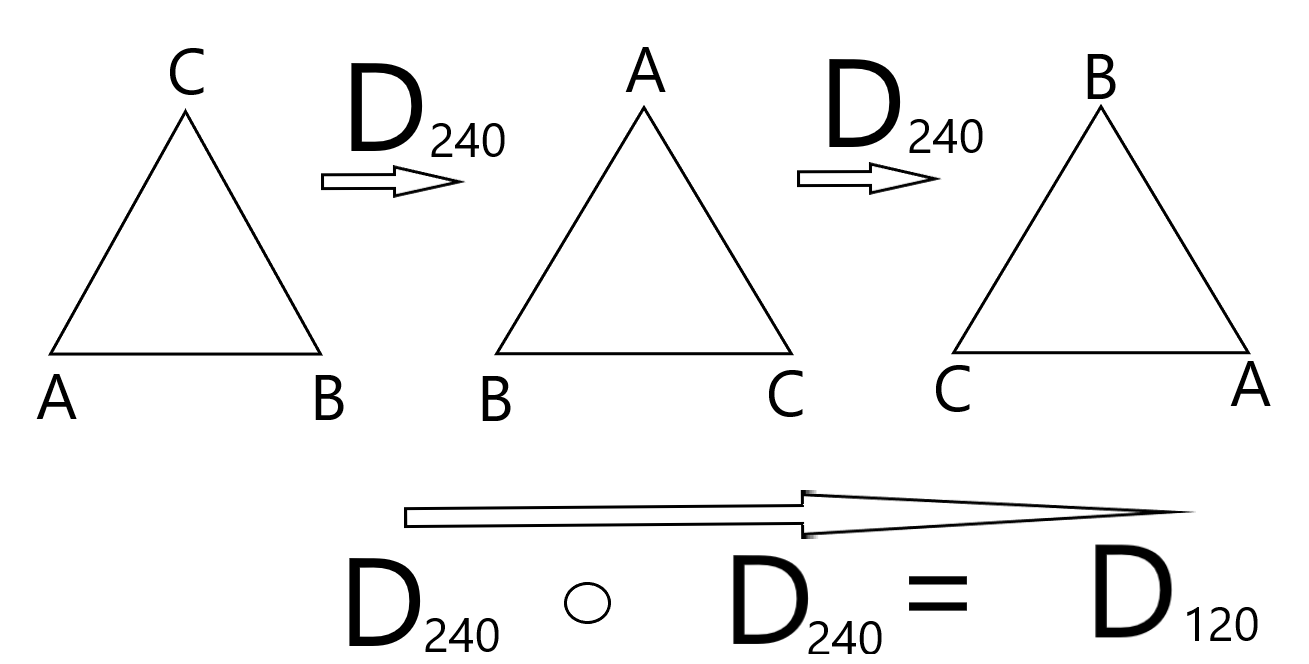
Die Menge besteht aus 3 Elementen: M = {D₀ , D₁₂₀ , D₂₄₀}. Die Verknüpfung ist HEA - die Hintereinanderausführung zweier Drehungen.

Es gilt z.B.: D₂₄₀ ᵒ D₂₄₀ = D₁₂₀.

Aufgabe: Erstelle eine Verknüpfungstafel der Drehgruppe.

HEA	D₀	D₁₂₀	D₂₄₀
D₀	D₀	D₁₂₀	D₂₄₀
D₁₂₀	D₁₂₀	D₂₄₀	D₀
D₂₄₀	D₂₄₀	D₀	D₁₂₀

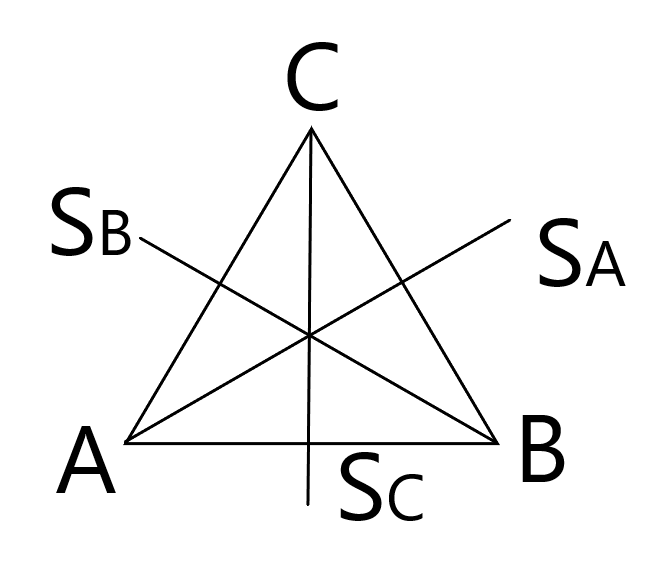
Zu den Drehungen fügen wir nun noch Spiegelungen S_A, S_B und S_C,an den Seitenhalbierenden bzw. Mittelsenkrechten hinzu. Diese sind beim gleichseitigen Dreieck gleich. Die Spiegelachsen bleiben im Raum fix, werden also bei einer Drehung des Dreiecks nicht mitgedreht.

Die Anordnung der Eckpunkte des Dreiecks ist für ein Beispiel unten abgebildet. Man erkennt: Der Drehsinn der Eckpunkte verändert sich bei einer Spiegelung im Gegensatz zu einer Drehung.

Die Verkettung einer Drehung und einer Spiegelung ist dem zweiten Bild zu entnehmen.

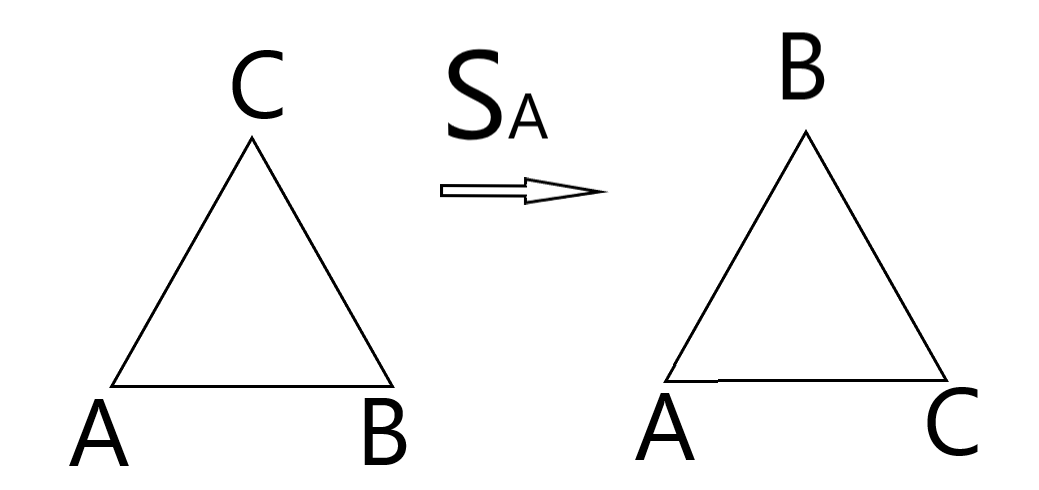
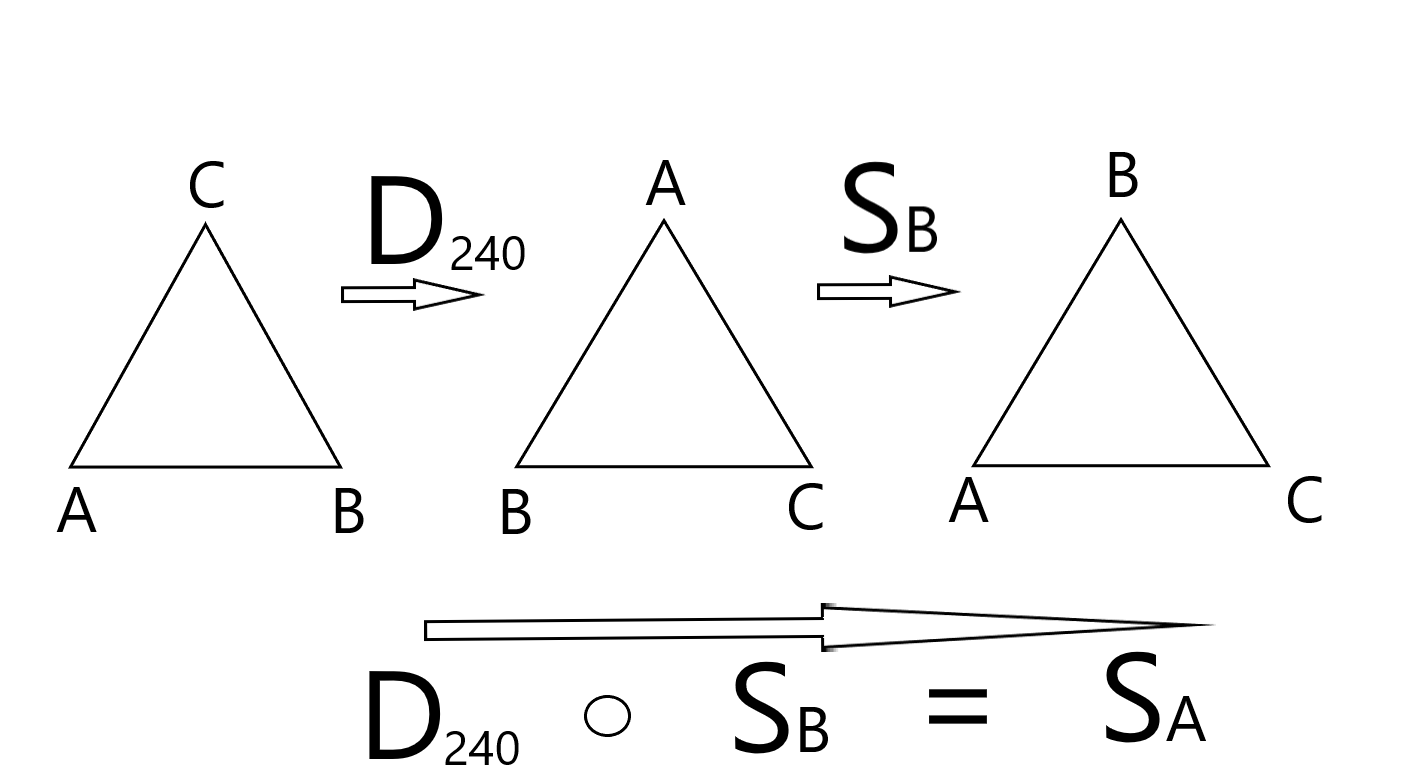
Wir betrachten nun die Menge M = {D₀ , D₁₂₀ , D₂₄₀, S_A, S_B, S_C}. Die Verknüpfung ist ebenfalls HEA.

Aufgabe: Erstelle eine Verknüpfungstafel der Dreh- und Spiegelgruppe M

HEA	D₀	D₁₂₀	D₂₄₀	S_A	S_B	S_C
D₀	D₀	D₁₂₀	D₂₄₀	S_A	S_B	S_C
D₁₂₀	D₁₂₀	D₂₄₀	D₀	S_B	S_C	S_A
D₂₄₀	D₂₄₀	D₀	D₁₂₀	S_C	S_A	S_B
S_A	S_A	S_C	S_B	D₀	D₂₄₀	D₁₂₀
S_B	S_B	S_A	S_C	D₁₂₀	D₀	D₂₄₀
S_C	S_C	S_B	S_A	D₂₄₀	D₁₂₀	D₀

Spiegelungen sind involutorisch. Es gilt nicht das Kommutativgesetz, denn z.B. D₁₂₀ ᵒ S_A ≠ S_A ᵒ D₁₂₀.

Teilmengen der Menge M bilden sogenannte Untergruppen von M.

Beispiele: {D₀,S_A} oder {D₀ , D₁₂₀ , D₂₄₀}

Aufgabe: Gib weitere Teilmengen an.

Noch ein Beispiel:

Lineare Funktionen der Form f(x) = a x + b mit a,b ∈ R , a ≠ 0 bilden mit der Hintereinanderausführung ebenfalls eine (nicht kommutative) Gruppe.

Seien f: x → 2x + 1 und g: x → 3x - 4, dann ist (f ᵒ g) (x) = f(g(x)) = 2 (3x - 4) + 1 = 6x - 7 ebenfalls eine lin Funktion.

Allgemein:

f: x → a₁x + b₁ und g: x → a₂x + b₂, dann gilt (f ᵒ g) (x) = f(g(x)) = a₁ (a₂x + b₂) + b₁ = a₁ a₂x + a₁b₂ + b₁

a₁ a₂ sowie a₁b₂ + b₁ sind ebenfalls reelle Zahlen. Damit ist die Abgeschlossenheit erfüllt.

Aufgaben:

1. Benenne das neutrale Element in der Menge der lin. Funktionen.

2. Benenne das inverse Element zu f(x) = ax + b, a ≠ 0 .

3. Gib mindestens ein Beispiel an für die Nichteinhaltung der Kommutativität der lin. Funktionen.

4. Gib Untergruppen in der Menge der linearen Funktionen an.

5. Bildet die Menge der quadratischen Funktionen f(x) = a x² + b x + c mit a,b,c ∈ R mit der Hintereinanderausführung eine Gruppe?

ad 1: Das neutrale Element ist die identische Abbildung: f(x) = x. Die identische Abbildung wird auch id genannt.

ad 2: Das inverse Element der Funktion f ist die Umkehrfunktion f^-1 (daher die Schreibweise der Umkehrfunktion). Um die Umkehrfunktion zu erhalten, müssen bekanntlich x und y getauscht werden. Dann ist nach y aufzulösen.

Dann erhält man f^-1(x) = 1/a x - b/a.

ad 3: Sei f(x) = x + 1 und g(x) = 2x. Dann ist (f ᵒ g) (x) = f(g(x)) = 2x + 1 und (g ᵒ f) (x) = g(f(x)) = 2 (x + 1) = 2x + 2.

4. Die einelementige Untergruppe, die aus dem neutralen Element besteht, ist immer eine (triviale) Untergruppe, ebenfalls die Menge selbst. Echte Untergruppen sind Funktionen der Form f(x) = ax (also b = 0) sowie Funktionen der Form f(x) = x + b (also a = 1).

ad 5. Diese Menge bildet keine Gruppe mit HEA. Sei f(x) = g(x) = x². Dann ist (f ᵒ g) (x) = f(g(x)) =x⁴ . Die Abgeschlossenheit ist nicht erfüllt.

Hingegen bildet die Menge aller ganzrationalen Funktionen mit HEA eine Gruppe.

Und zumSchluss.

Es erfolgt noch der einfache Beweis eines Satzes, der für beliebige Gruppen gilt:

Die Nummern als Begründung der einzelnen Umwandlungsschritte beziehen sich auf die Gruppenaxiome:

1 Abgeschlossenheit , 2 Assoziativgesetz , 3 neutr. Element , 4. inverses Element.

Behauptung: Gegeben sei eine Gruppe.

Dann ist das Rechtsinverse gleich dem Linksinversen: a ◦ a^-1 = n = a^-1 ◦ a

und das Rechtsneutrale gleich dem Linksneutralen: a ◦ n = a = n ◦ a

Anmerkung: im Fall einer abelschen Gruppe trivial.

Beweis: (*) a^-1 ◦ a ◦ a^-1 = a^-1 ◦ n = a^-1 mit (2 , 3)

Multipliziert man (*) von rechts mit dem Inversen von a^-1 : (a^-1)^-1

a^-1 ◦ a ◦ a^-1 ◦ (a^-1)^-1 = a^-1 ◦ (a^-1)^-1 Mit (2 , 4) erhält man

a^-1 ◦ a ◦ n = n mit (2 , 3 , 4) folgt

(**) a^-1 ◦ a = a ◦ a^-1 → 1. Teil der Behauptung: linksinvers = rechtsinvers

Dann ist es einfach:

n ◦ a = a ◦ a^-1 ◦ a mit (2 , 4)

= a ◦ n mit (**) → 2. Teil: linksneutral = rechtsneutral